Zadaci čije je rješenje transformacija logaritamski izrazi , prilično su česti na Jedinstvenom državnom ispitu.

Da biste se uspješno nosili s njima uz minimalno vrijeme, pored osnovnih logaritamskih identiteta, potrebno je znati i pravilno koristiti još neke formule.

Ovo je: a log a b = b, gdje je a, b > 0, a ≠ 1 (direktno slijedi iz definicije logaritma).

log a b = log c b / log c a ili log a b = 1/log b a
gdje su a, b, c > 0; a, c ≠ 1.

log a m b n = (m/n) log |a| |b|
gdje su a, b > 0, a ≠ 1, m, n Ê R, n ≠ 0.

a log c b = b log c a
gdje su a, b, c > 0 i a, b, c ≠ 1

Da bismo pokazali valjanost četvrte jednakosti, uzmimo logaritam lijeve i desne strane na osnovu a. Dobijamo log a (a log sa b) = log a (b log sa a) ili log sa b = log sa a · log a b; log c b = log c a · (log c b / log c a); log sa b = log sa b.

Dokazali smo jednakost logaritama, što znači da su i izrazi pod logaritmima jednaki. Formula 4 je dokazana.

Primjer 1.

Izračunaj 81 log 27 5 log 5 4 .

Rješenje.

81 = 3 4 , 27 = 3 3 .

log 27 5 = 1/3 log 3 5, log 5 4 = log 3 4 / log 3 5. Dakle,

log 27 5 log 5 4 = 1/3 log 3 5 (log 3 4 / log 3 5) = 1/3 log 3 4.

Tada je 81 log 27 5 log 5 4 = (3 4) 1/3 log 3 4 = (3 log 3 4) 4/3 = (4) 4/3 = 4 3 √4.

Sljedeći zadatak možete izvršiti sami.

Izračunaj (8 log 2 3 + 3 1/ log 2 3) - log 0,2 5.

Kao nagoveštaj, 0,2 = 1/5 = 5 -1; log 0,2 5 = -1.

Odgovor: 5.

Primjer 2.

Izračunaj (√11) log √3 9- log 121 81 .

Rješenje.

Promenimo izraze: 9 = 3 2, √3 = 3 1/2, log √3 9 = 4,

121 = 11 2, 81 = 3 4, log 121 81 = 2 log 11 3 (korišćena je formula 3).

Tada (√11) log √3 9- log 121 81 = (11 1/2) 4-2 log 11 3 = (11) 2- log 11 3 = 11 2 / (11) log 11 3 = 11 2 / ( 11 log 11 3) = 121/3.

Primjer 3.

Izračunajte log 2 24 / log 96 2 - log 2 192 / log 12 2.

Rješenje.

Logaritme sadržane u primjeru zamjenjujemo logaritmima s bazom 2.

log 96 2 = 1/log 2 96 = 1/log 2 (2 5 3) = 1/(log 2 2 5 + log 2 3) = 1/(5 + log 2 3);

log 2 192 = log 2 (2 6 3) = (log 2 2 6 + log 2 3) = (6 + log 2 3);

log 2 24 = log 2 (2 3 3) = (log 2 2 3 + log 2 3) = (3 + log 2 3);

log 12 2 = 1/log 2 12 = 1/log 2 (2 2 3) = 1/(log 2 2 2 + log 2 3) = 1/(2 + log 2 3).

Zatim log 2 24 / log 96 2 – log 2 192 / log 12 2 = (3 + log 2 3) / (1/(5 + log 2 3)) – ((6 + log 2 3) / (1/( 2 + log 2 3)) =

= (3 + log 2 3) · (5 + log 2 3) – (6 + log 2 3)(2 + log 2 3).

Nakon otvaranja zagrada i donošenja sličnih pojmova, dobijamo broj 3. (Kada pojednostavljujemo izraz, možemo označiti log 2 3 sa n i pojednostaviti izraz

(3 + n) · (5 + n) – (6 + n)(2 + n)).

Odgovor: 3.

Sljedeći zadatak možete izvršiti sami:

Izračunaj (log 3 4 + log 4 3 + 2) log 3 16 log 2 144 3.

Ovdje je potrebno izvršiti prijelaz na logaritma baze 3 i faktorizaciju velikih brojeva u proste faktore.

Odgovor:1/2

Primjer 4.

Zadata su tri broja A = 1/(log 3 0,5), B = 1/(log 0,5 3), C = log 0,5 12 – log 0,5 3. Rasporedi ih rastućim redoslijedom.

Rješenje.

Transformirajmo brojeve A = 1/(log 3 0,5) = log 0,5 3; C = log 0,5 12 – log 0,5 3 = log 0,5 12/3 = log 0,5 4 = -2.

Hajde da ih uporedimo

log 0,5 3 > log 0,5 4 = -2 i log 0,5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.

Ili 2< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.

Odgovori. Dakle, redosled postavljanja brojeva je: C; A; IN.

Primjer 5.

Koliko je cijelih brojeva u intervalu (log 3 1 / 16 ; log 2 6 48).

Rješenje.

Odredimo između kojih stepena broja 3 se nalazi broj 1/16. Dobijamo 1/27< 1 / 16 < 1 / 9 .

Budući da je funkcija y = log 3 x u porastu, onda je log 3 (1 / 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.

log 6 48 = log 6 (36 4 / 3) = log 6 36 + log 6 (4 / 3) = 2 + log 6 (4 / 3). Uporedimo log 6 (4/3) i 1/5. I za ovo upoređujemo brojeve 4/3 i 6 1/5. Podignimo oba broja na 5. stepen. Dobijamo (4 / 3) 5 = 1024 / 243 = 4 52 / 243< 6. Следовательно,

log 6 (4 / 3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.

Dakle, interval (log 3 1 / 16 ; log 6 48) uključuje interval [-2; 4] i na njega se stavljaju cijeli brojevi -2; -1; 0; 1; 2; 3; 4.

Odgovor: 7 cijelih brojeva.

Primjer 6.

Izračunajte 3 lglg 2/lg 3 - lg20.

Rješenje.

3 lg lg 2/ lg 3 = (3 1/ lg3) lg lg 2 = (3 lo g 3 10) lg lg 2 = 10 lg lg 2 = lg2.

Tada je 3 lglg2/lg3 - lg 20 = lg 2 – lg 20 = lg 0,1 = -1.

Odgovor: -1.

Primjer 7.

Poznato je da je log 2 (√3 + 1) + log 2 (√6 – 2) = A. Pronađite log 2 (√3 –1) + log 2 (√6 + 2).

Rješenje.

Brojevi (√3 + 1) i (√3 – 1); (√6 – 2) i (√6 + 2) su konjugirani.

Izvršimo sljedeću transformaciju izraza

√3 – 1 = (√3 – 1) · (√3 + 1)) / (√3 + 1) = 2/(√3 + 1);

√6 + 2 = (√6 + 2) · (√6 – 2)) / (√6 – 2) = 2/(√6 – 2).

Tada log 2 (√3 – 1) + log 2 (√6 + 2) = log 2 (2/(√3 + 1)) + log 2 (2/(√6 – 2)) =

Log 2 2 – log 2 (√3 + 1) + log 2 2 – log 2 (√6 – 2) = 1 – log 2 (√3 + 1) + 1 – log 2 (√6 – 2) =

2 – log 2 (√3 + 1) – log 2 (√6 – 2) = 2 – A.

Odgovor: 2 – A.

Primjer 8.

Pojednostavite i pronađite približnu vrijednost izraza (log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9.

Rješenje.

Svedemo sve logaritme na zajedničku bazu 10.

(log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9 = (lg 2 / lg 3) (lg 3 / LG 4) (lg 4 / LG 5) (lg 5 / LG 6) · … · (lg 8 / lg 9) · lg 9 = lg 2 ≈ 0,3010 (Približna vrijednost lg 2 može se pronaći pomoću tabele, kliznog ravnala ili kalkulatora).

Odgovor: 0,3010.

Primjer 9.

Izračunajte log a 2 b 3 √(a 11 b -3) ako je log √ a b 3 = 1. (U ovom primjeru, a 2 b 3 je osnova logaritma).

Rješenje.

Ako je log √ a b 3 = 1, onda je 3/(0,5 log a b = 1. I log a b = 1/6.

Tada log a 2 b 3√(a 11 b -3) = 1/2 log a 2 b 3 (a 11 b -3) = log a (a 11 b -3) / (2log a (a 2 b 3) ) = (log a a 11 + log a b -3) / (2(log a a 2 + log a b 3)) = (11 – 3log a b) / (2(2 + 3log a b)) S obzirom da je log a b = 1/ 6 dobijamo (11 – 3 1 / 6) / (2(2 + 3 1 / 6)) = 10,5/5 = 2,1.

Odgovor: 2.1.

Sljedeći zadatak možete izvršiti sami:

Izračunajte log √3 6 √2.1 ako je log 0.7 27 = a.

Odgovor: (3 + a) / (3a).

Primjer 10.

Izračunajte 6,5 4/ log 3 169 · 3 1/ log 4 13 + log125.

Rješenje.

6.5 4/ log 3 169 · 3 1/ log 4 13 + log 125 = (13/2) 4/2 log 3 13 · 3 2/ log 2 13 + 2log 5 5 3 = (13/2) 2 log 13 3 3 2 log 13 2 + 6 = (13 log 13 3 / 2 log 13 3) 2 (3 log 13 2) 2 + 6 = (3/2 log 13 3) 2 (3 log 13 2) 2 + 6 = ( 3 2 /(2 log 13 3) 2) · (2 ​​log 13 3) 2 + 6.

(2 log 13 3 = 3 log 13 2 (formula 4))

Dobijamo 9 + 6 = 15.

Odgovor: 15.

Imate još pitanja? Niste sigurni kako pronaći vrijednost logaritamskog izraza?
Da biste dobili pomoć od tutora, registrujte se.
Prva lekcija je besplatna!

web stranicu, kada kopirate materijal u cijelosti ili djelomično, link na izvor je obavezan.

Logaritamski izrazi, primjeri rješavanja. U ovom članku ćemo se osvrnuti na probleme vezane za rješavanje logaritama. U zadacima se postavlja pitanje pronalaženja značenja izraza. Treba napomenuti da se koncept logaritma koristi u mnogim zadacima i razumijevanje njegovog značenja je izuzetno važno. Što se tiče Jedinstvenog državnog ispita, logaritam se koristi pri rješavanju jednačina, u primijenjenim problemima, kao i u zadacima vezanim za proučavanje funkcija.

Navedimo primjere kako bismo razumjeli samo značenje logaritma:

Osnovni logaritamski identitet:

Svojstva logaritama koje se uvijek moraju zapamtiti:

*Logaritam proizvoda jednak je zbiru logaritama faktora.

* * *

*Logaritam količnika (razlomka) jednak je razlici između logaritama faktora.

* * *

*Logaritam eksponenta jednak je proizvodu eksponenta i logaritma njegove baze.

* * *

*Prelazak na novu osnovu

* * *

Više nekretnina:

* * *

Izračunavanje logaritama je usko povezano sa upotrebom svojstava eksponenata.

Navedimo neke od njih:

Suština ovog svojstva je da kada se brojnik prenese na nazivnik i obrnuto, predznak eksponenta se mijenja u suprotan. Na primjer:

Zaključak iz ove nekretnine:

* * *

Kada se stepen diže na stepen, baza ostaje ista, ali se eksponenti množe.

* * *

Kao što ste vidjeli, sam koncept logaritma je jednostavan. Glavna stvar je da vam je potrebna dobra praksa, koja vam daje određenu vještinu. Naravno, potrebno je poznavanje formula. Ako vještina pretvaranja elementarnih logaritama nije razvijena, tada prilikom rješavanja jednostavnih zadataka možete lako pogriješiti.

Vježbajte, prvo riješite najjednostavnije primjere iz matematike, pa pređite na složenije. U budućnosti ću svakako pokazati kako se rješavaju "strašni" logaritmi neće se pojaviti na Jedinstvenom državnom ispitu, ali su zanimljivi, nemojte ih propustiti!

To je sve! Sretno ti!

Srdačan pozdrav, Alexander Krutitskikh

P.S: Bio bih vam zahvalan ako mi kažete nešto o stranici na društvenim mrežama.

EGOROVA VICTORIA VALERIEVNA

Nastavnik matematike

najviša kvalifikaciona kategorija

TEMA: “IDENTALNA TRANSFORMACIJA

LOGARITAMSKI IZRAZI"

Znanja i vještine kojima studenti treba da ovladaju nakon studija ovu lekciju:

poznaju definiciju logaritma broja, osnovni logaritamski identitet, svojstva logaritma;

biti u stanju izvršiti transformacije izraza koji sadrže logaritme i izračunati logaritme.

književnost:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. i dr. Algebra i počeci analize: udžbenik za 10-11 razred opšteobrazovnih ustanova. – M.: Obrazovanje, 2001.

2. Kočagin V.V., Kočagina M.V., Intenzivni pripremni kurs za Jedinstveni državni ispit. – M.: Eksmo, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Algebarski simulator: Priručnik za školarce i kandidate. – M.: Ilexa, 2005.

4. Gusev V.A., Mordkovich A.G. matematika: Referentni materijali: Knjiga za studente. – M.: Obrazovanje, 2001.

Plan lekcije:

Tokom nastave:

1) Logaritam je grčka riječ koja se sastoji od 2 riječi: “logos” - omjer, "arithmos" - broj. To znači da je logaritam broj koji mjeri omjer. Publikacija iz 1614. objavila je da je Napier izmislio logaritme. Kasnije je sastavio logaritamske tabele, koje su nam danas poznate kao Bradisove tabele. Za manje od jednog vijeka, tablice su se proširile po cijelom svijetu i postale nezamjenjiv računarski alat. Nakon toga su, takoreći, ugrađeni u zgodan uređaj koji uvelike ubrzava proces izračunavanja - klizač, koji se koristio do sedamdesetih godina dvadesetog stoljeća.

Aneks 1.

2) Logaritam pozitivan brojb na osnovu a, i A Iznad nule a nije jednako jednom,je eksponent na koji se broj mora podićia da dobijem brojb.

Ova jednakost, koja izražava definiciju logaritma, naziva seosnovni logaritamski identitet .

C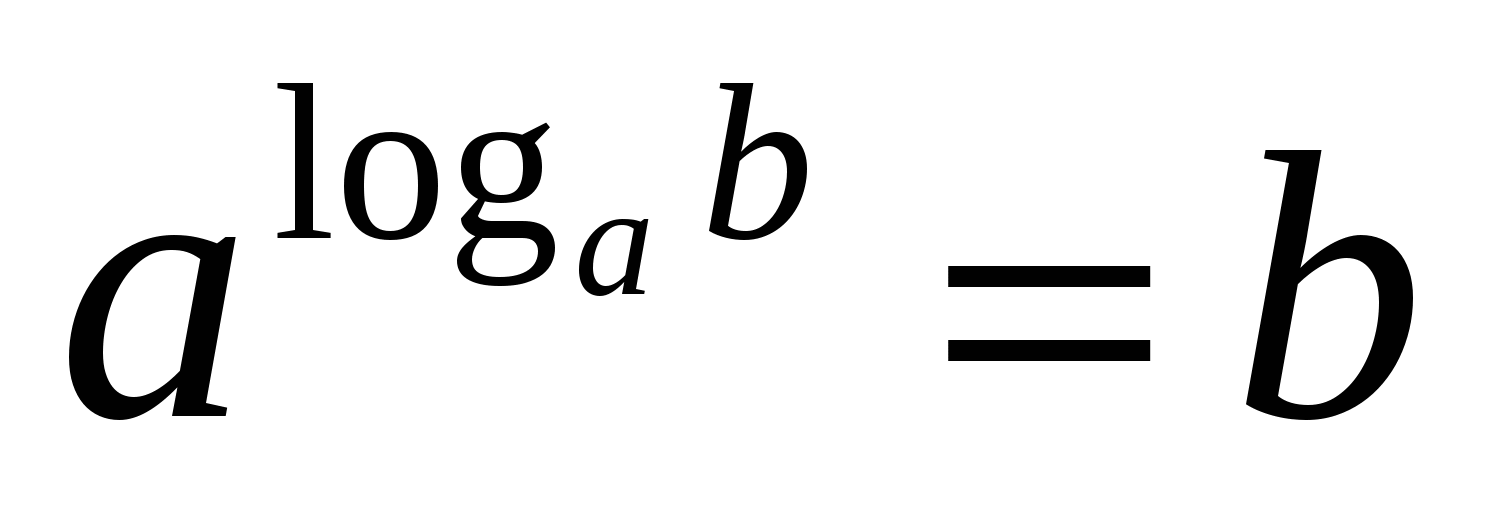

ILI 1

P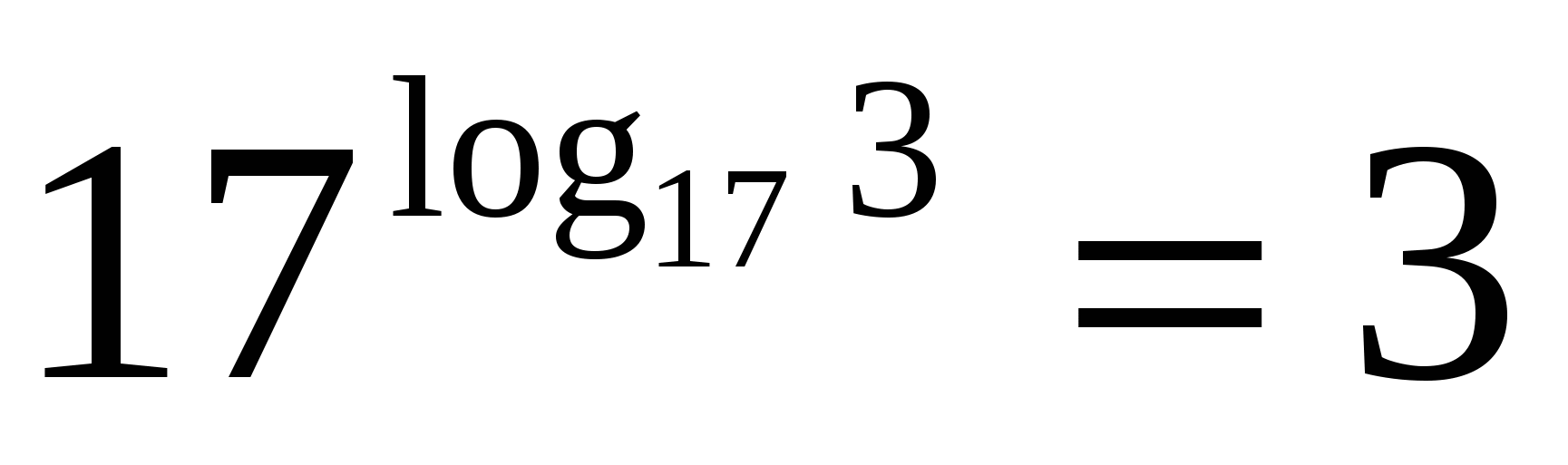

Osnova stepena i osnova logaritma su sedamnaest, što znači da je prema osnovnom logaritamskom identitetu vrijednost izraza tri.

Hajde da to radimo usmeno:

SCH
FIR-BELLE

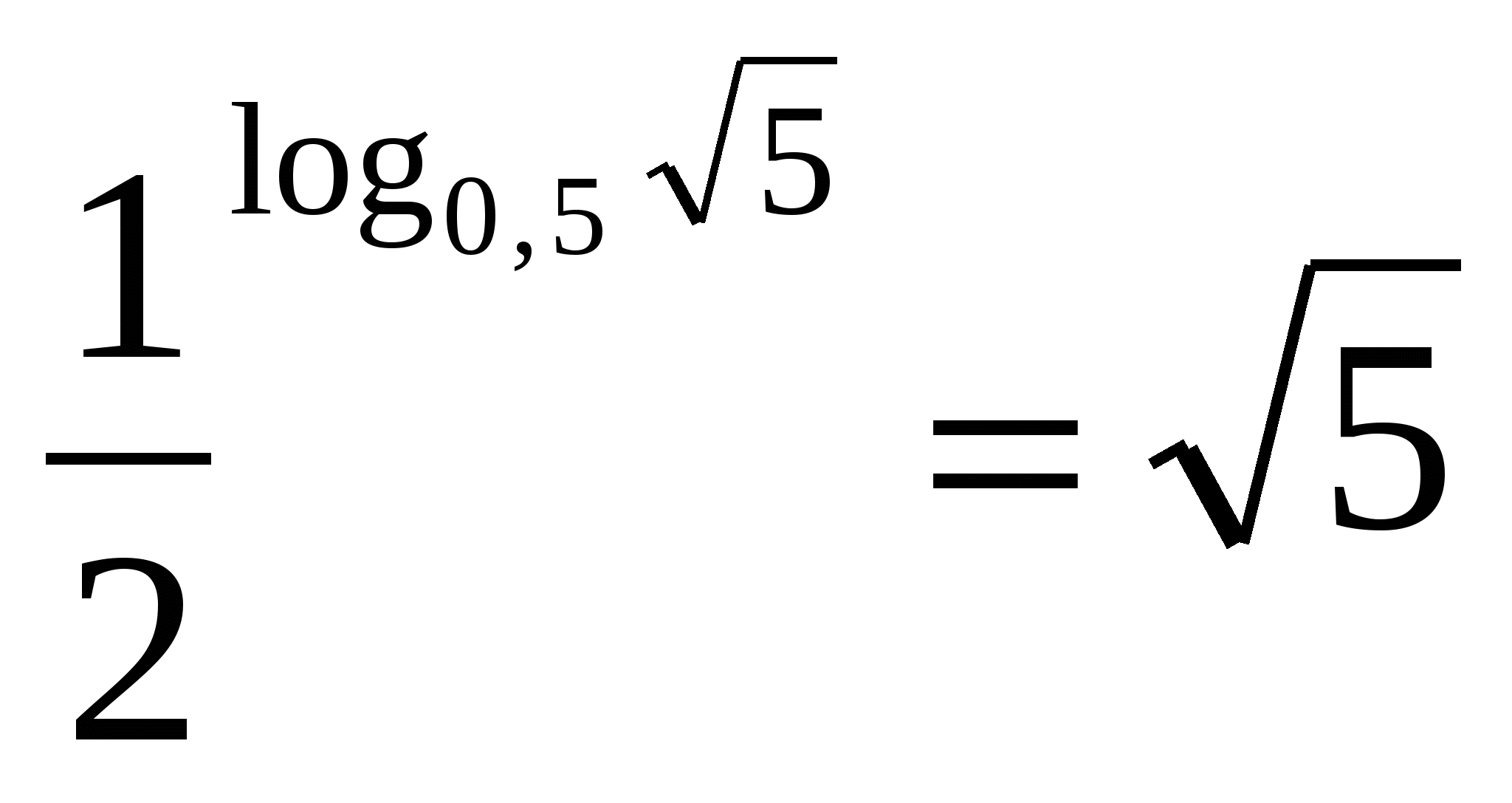
O dno sekunde je jednako nula tački pet, što znači da je izraz jednak aritmetici kvadratni korijen od pet.

P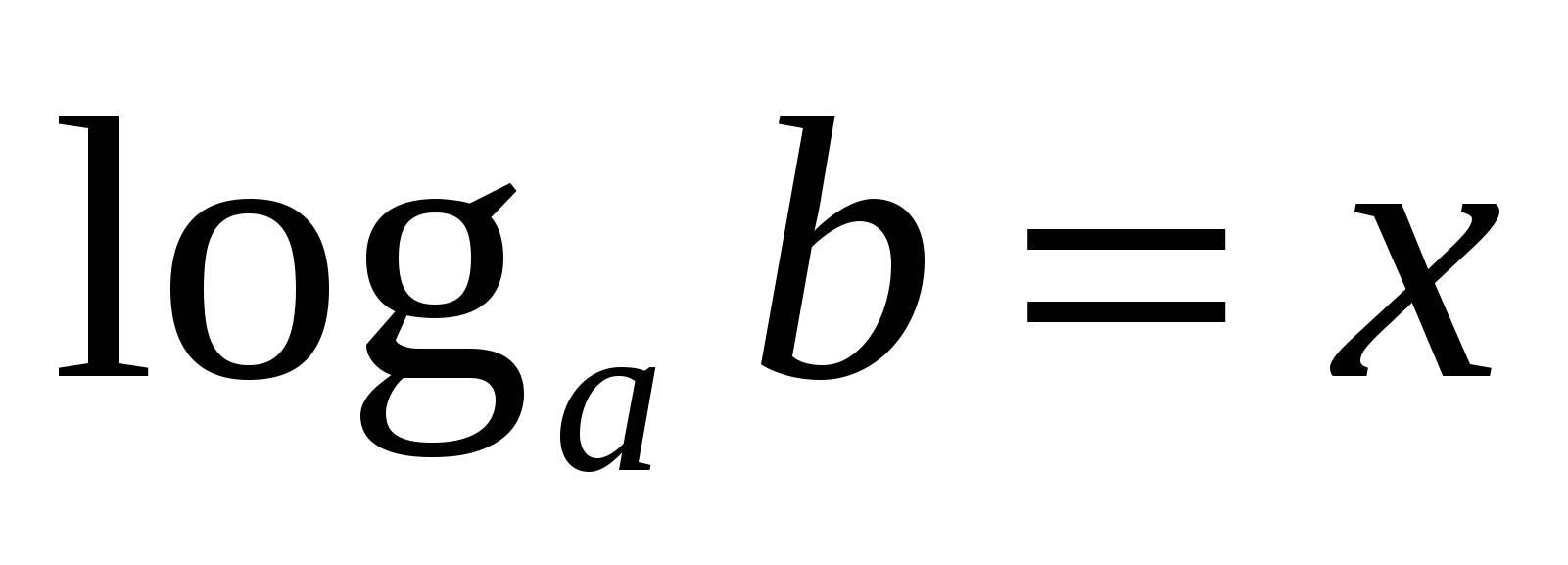

Dodatak 2.

Jednakost znači da

Iz definicije logaritma dobijaju se sljedeće važne jednakosti:

Na primjer:

P
Dodatak 3.

Idemo dalje Zadaci objedinjenog državnog ispita:

Dodatak 4.

3
) Postoji posebna oznaka i naziv za logaritam baze desetdecimalni logaritam .

L
bazni kalaritame pozvaoprirodni logaritam .

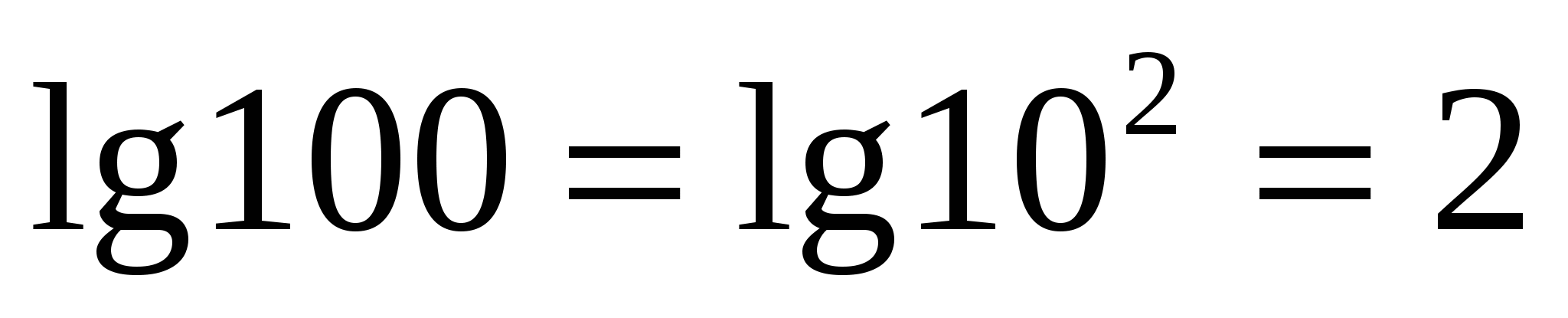
N
na primjer,

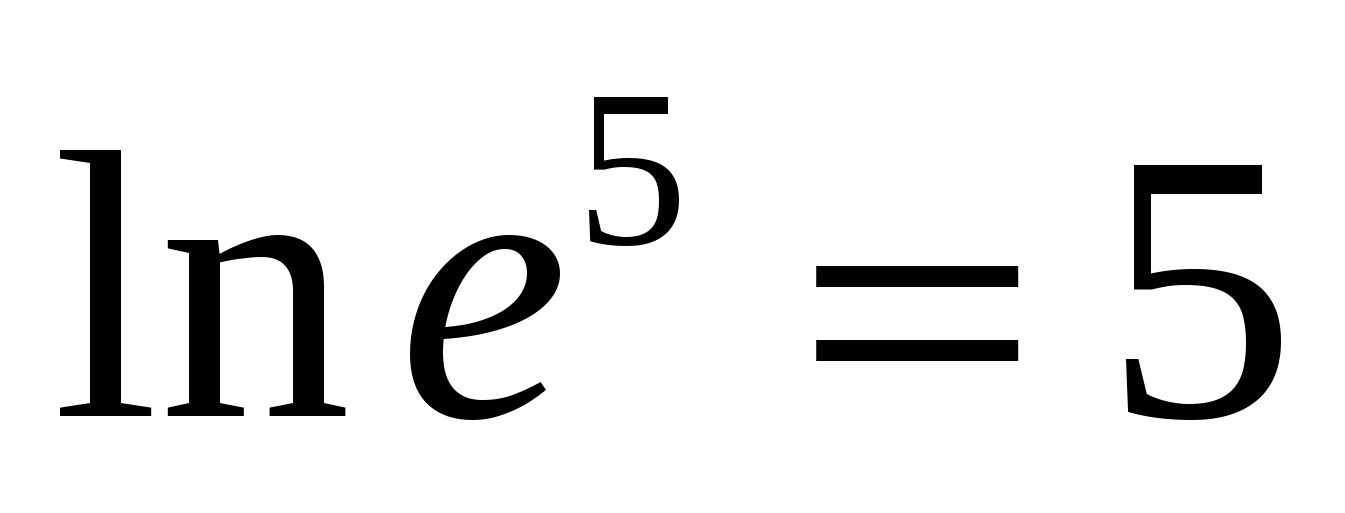
4) Iz definicije logaritma slijede sljedeća svojstva. Sva svojstva su formulirana i dokazana samo za pozitivne vrijednosti varijable sadržane pod logaritamskim predznacima.

Logaritam proizvoda dva pozitivna broja na bazu A jednak zbiru logaritama ovih brojeva sa istom bazom.

TsOR 2

Na primjer,

Z
zadatak 1.

Zadatak 2. Pojednostavite izraz

IN
Koristimo rješenje prethodnog primjera. Zamenićemo

Imajte na umu da je logaritam na kvadrat, tako da se zbir mora kvadrirati. Koristeći formulu za kvadrat zbira, otvaramo zagrade. Hajde da predstavimo slične pojmove.

5) Logaritam količnika jednak je razlici između logaritama dividende i djelitelja.

C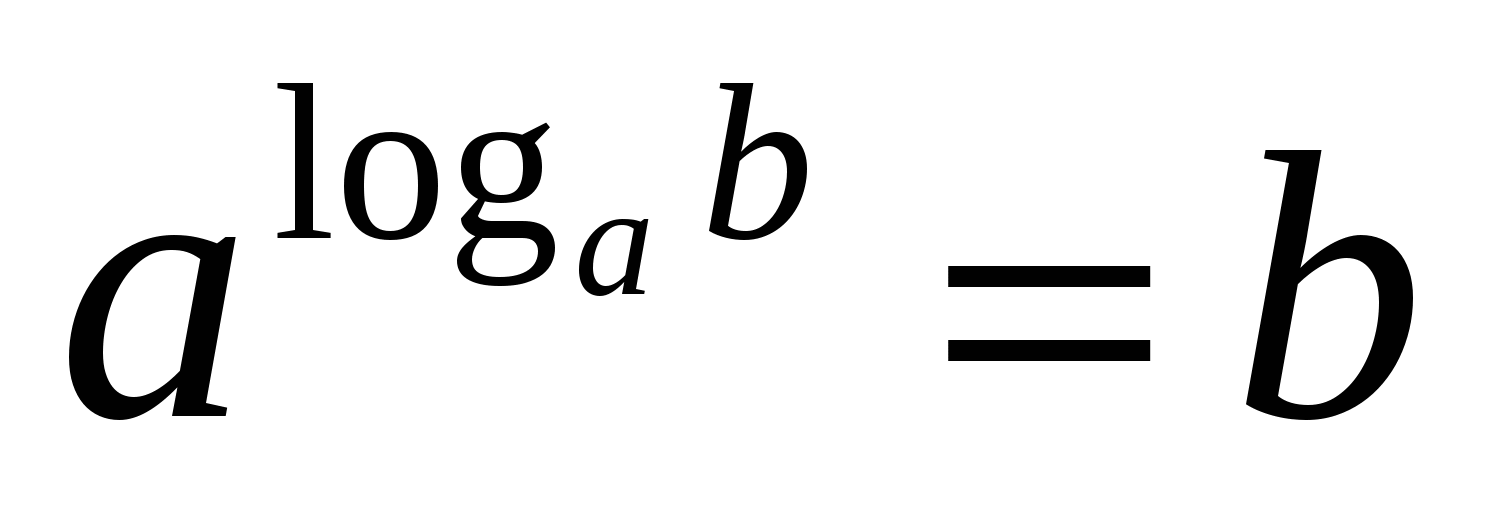

Obratite pažnju na bazu stepena i bazu logaritma - iste su.

ILI 3

R

Pogledajmo primjenu ove formule koristeći primjer:

Z
zadatak 1. Pronađite vrijednost izraza if

Zadatak 2. Pronađite vrijednost b po svom logaritmu

6) Logaritam stepena prema baziA , jednak je proizvodu eksponenta i logaritma koristeći istu bazu.

TsOR 4

Na primjer,

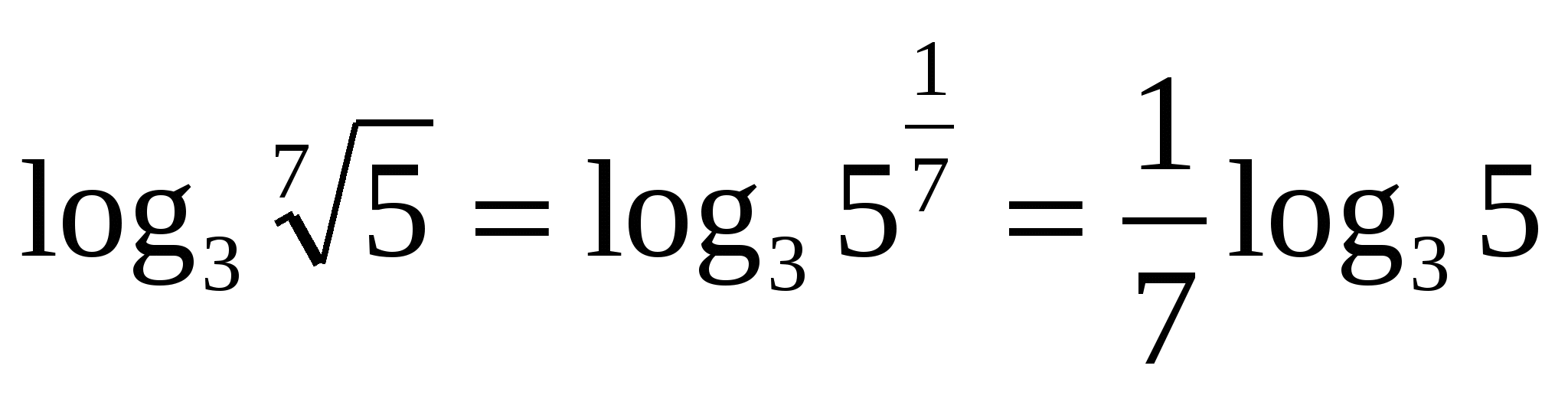
Z
zadatak 1. Izračunajte ako

Hajde da pojednostavimo izraz

Formula

pozvao formula za prelazak na novu osnovu.

Z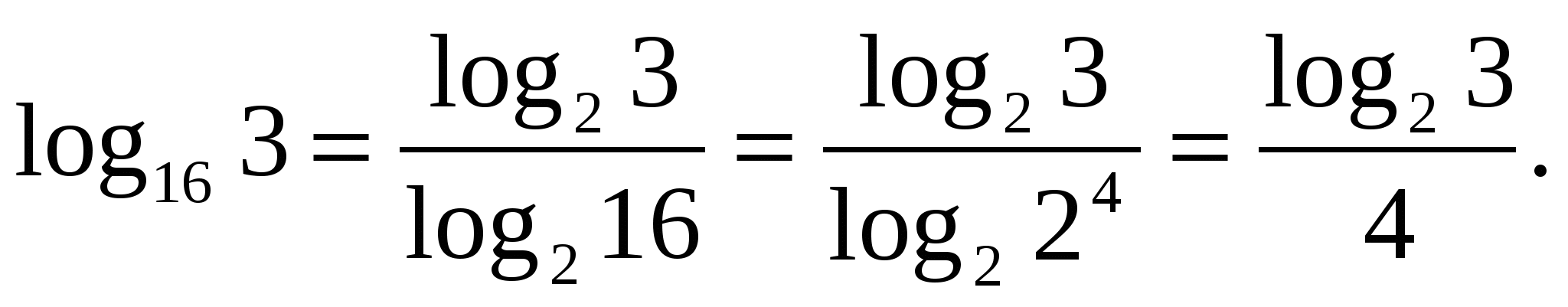

zadatak 1. Izrazite koristeći logaritam sa bazom 2.

Zadatak 2. Izračunati

TsOR 5

TsOR 6

Na primjer,

Z

zadatak 1. Izračunati

Z
zadatak 2. Izračunati

9) Logaritamske transformacije se mogu započeti samo u slučajevima kada ako se sjetite svih svojstava logaritama. Nakon što ih ponovimo, razmotrit ćemo zadatke za transformaciju logaritamskih izraza s druge strane.

Za pretvaranje sume ili razlike logaritamskih izraza ponekad je dovoljno koristiti definiciju logaritma, a najčešće svojstva logaritma proizvoda ili količnika.

Z
zadatak 1. Izračunati

Hajde da to riješimo na dva načina.

1 način, koristeći definiciju logaritma:

Metoda 2, zasnovana na svojstvo logaritma količnika:

Zadatak 2. Pronađite značenje izraza

Prvo primijenimo formulu logaritam proizvoda, zatim definicija logaritma.

Osnovni logaritamski identitet se koristi kada se pretvaraju izrazi koji sadrže logaritam kao eksponent. Ideja ovakvih operacija je da se dobiju jednake baze potencija i baza logaritma.

Ponekad je potrebno transformisati izraz po svojstvima logaritma i svojstvima stepena, takođe možete lako prelaziti s jedne baze na drugu koristeći prijelaznu formulu. U drugim slučajevima treba primijeniti više svojstava.

Z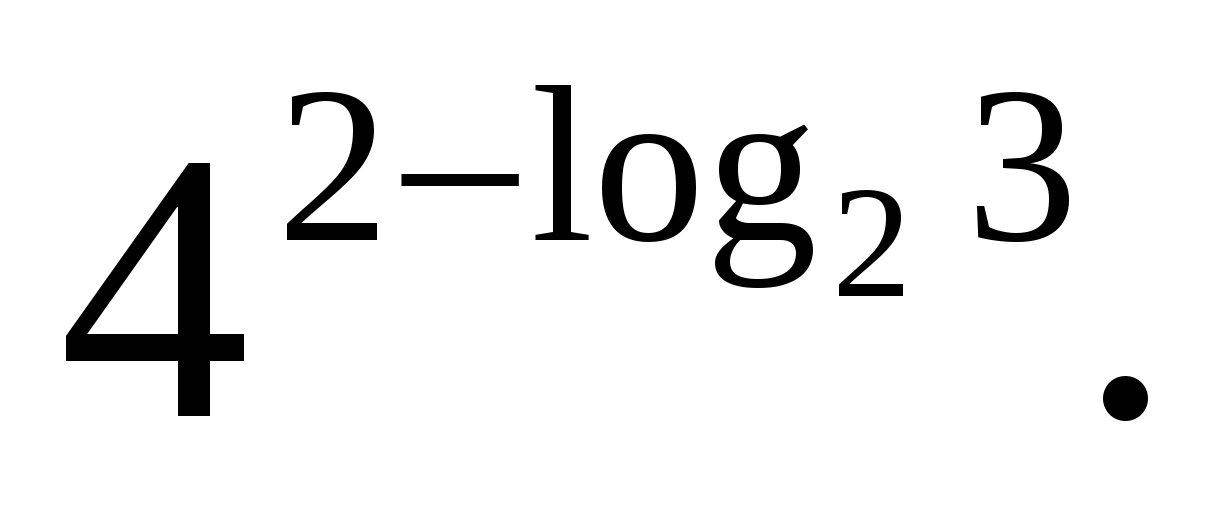
zadatak 3. Izračunati

Z
zadatak 4. Pronađite značenje izraza

Zadatak 5. Pronađite značenje izraza

Z
zadatak 6. Izrazite to kao razliku logaritama

N
Najveća poteškoća je u pretvaranju logaritamskih izraza pod radikal. U procesu transformacija potrebno je razmotriti module logaritamskih izraza za čije je otkrivanje potrebno uporediti iracionalne brojeve ili racionalne i iracionalan broj. Mi ćemo djelovati dosljedno. Pogledajmo izraz ispod unutrašnjeg radikala.

Zamijenimo ga u originalni izraz.

Treba napomenuti da se transformacija logaritamskih izraza može susresti i pri rješavanju jednadžbi i nejednačina ili proučavanju funkcija, pa mogu biti prisutni u implicitnom obliku u zadacima grupa B i C.

10) Rezimiranje pitanja:

Poziva se logaritam na osnovu 10

osnovni logaritam

glavni logaritam

prirodni logaritam

decimalni logaritam

2) Koje vrijednosti može poprimiti?x u izrazu

Vrijednost nije definirana

5) Dajte omjer koji vrijedi za svex ≠ 0 .

6) Navedite tačan odnos za formulu za prelazak na novu bazu.

7) Navedite tačnu jednakost za

11) Kontrolno testiranje.

Logaritmi se, kao i svi brojevi, mogu sabirati, oduzimati i transformirati na sve načine. Ali pošto logaritmi nisu baš obični brojevi, ovdje postoje pravila koja se nazivaju glavna svojstva.

Svakako morate znati ova pravila - bez njih se ne može riješiti nijedan ozbiljan logaritamski problem. Osim toga, vrlo ih je malo - sve možete naučiti u jednom danu. Pa počnimo.

Sabiranje i oduzimanje logaritama

Razmotrimo dva logaritma sa istim osnovama: log a x i log a y. Tada se mogu sabirati i oduzimati i:

1. log a x+ log a y=log a (x · y);
2. log a x− log a y=log a (x : y).

Dakle, zbir logaritama je jednak logaritmu proizvoda, a razlika je jednaka logaritmu količnika. Imajte na umu: ključna stvar je ovdje identične osnove. Ako su razlozi drugačiji, ova pravila ne funkcionišu!

Ove formule će vam pomoći da izračunate logaritamski izraz čak i kada se njegovi pojedinačni dijelovi ne uzimaju u obzir (pogledajte lekciju “Šta je logaritam”). Pogledajte primjere i pogledajte:

Dnevnik 6 4 + log 6 9.

Pošto logaritmi imaju iste baze, koristimo formulu sume:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadatak. Pronađite vrijednost izraza: log 2 48 − log 2 3.

Osnove su iste, koristimo formulu razlike:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadatak. Pronađite vrijednost izraza: log 3 135 − log 3 5.

Opet su baze iste, tako da imamo:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kao što vidite, originalni izrazi su sastavljeni od „loših“ logaritama, koji se ne računaju zasebno. Ali nakon transformacija dobijaju se sasvim normalni brojevi. Mnogi su izgrađeni na ovoj činjenici test papiri. Da, izrazi poput testa se nude sa punom ozbiljnošću (ponekad bez ikakvih promjena) na Jedinstvenom državnom ispitu.

Izdvajanje eksponenta iz logaritma

Sada da malo zakomplikujemo zadatak. Šta ako je osnova ili argument logaritma potencija? Tada se eksponent ovog stepena može izvaditi iz predznaka logaritma prema sljedećim pravilima:

Lako je vidjeti da posljednje pravilo slijedi prva dva. Ali ipak je bolje zapamtiti to - u nekim slučajevima to će značajno smanjiti količinu izračuna.

Naravno, sva ova pravila imaju smisla ako se poštuje ODZ logaritma: a > 0, a ≠ 1, x> 0. I još nešto: naučite primjenjivati ​​sve formule ne samo s lijeva na desno, već i obrnuto, tj. Brojeve prije znaka logaritma možete unijeti u sam logaritam. To je ono što se najčešće traži.

Zadatak. Pronađite vrijednost izraza: log 7 49 6 .

Oslobodimo se stepena u argumentu koristeći prvu formulu:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadatak. Pronađite značenje izraza:

[Natpis za sliku]

Imajte na umu da nazivnik sadrži logaritam, čija su osnova i argument tačni potenci: 16 = 2 4 ; 49 = 7 2. Imamo:

[Natpis za sliku]

Mislim da posljednji primjer zahtijeva pojašnjenje. Gdje su nestali logaritmi? Sve do samog poslednji trenutak radimo samo sa imeniocem. Osnovu i argument logaritma koji tu stoji predstavili smo u obliku stepena i iznijeli eksponente - dobili smo razlomak od tri sprata.

Pogledajmo sada glavni razlomak. Brojilac i imenilac sadrže isti broj: log 2 7. Pošto je log 2 7 ≠ 0, možemo smanjiti razlomak - 2/4 će ostati u nazivniku. Prema pravilima aritmetike, četvorka se može prenijeti u brojilac, što je i učinjeno. Rezultat je bio odgovor: 2.

Prelazak na novu osnovu

Govoreći o pravilima za sabiranje i oduzimanje logaritama, posebno sam naglasio da oni rade samo sa istim osnovama. Šta ako su razlozi drugačiji? Šta ako nisu tačne snage istog broja?

Formule za prelazak na novu podlogu dolaze u pomoć. Formulirajmo ih u obliku teoreme:

Neka je dat log logaritam a x. Zatim za bilo koji broj c takav da c> 0 i c≠ 1, jednakost je tačna:

[Natpis za sliku]

Konkretno, ako stavimo c = x, dobijamo:

[Natpis za sliku]

Iz druge formule proizilazi da se baza i argument logaritma mogu zamijeniti, ali se u ovom slučaju cijeli izraz „obrće“, tj. logaritam se pojavljuje u nazivniku.

Ove formule se rijetko nalaze u običnim numeričkim izrazima. Koliko su zgodne moguće je procijeniti samo odlučivanjem logaritamske jednačine i nejednakosti.

Međutim, postoje problemi koji se nikako ne mogu riješiti osim preseljenjem u novu osnovu. Pogledajmo par ovih:

Zadatak. Pronađite vrijednost izraza: log 5 16 log 2 25.

Imajte na umu da argumenti oba logaritma sadrže tačne potencije. Izvadimo indikatore: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Sada "obrnimo" drugi logaritam:

[Natpis za sliku]

Kako se proizvod ne mijenja pri preraspodjelu faktora, mirno smo pomnožili četiri i dva, a zatim se pozabavili logaritmima.

Zadatak. Pronađite vrijednost izraza: log 9 100 lg 3.

Osnova i argument prvog logaritma su tačni potenci. Zapišimo ovo i riješimo se indikatora:

[Natpis za sliku]

Sada se riješimo decimalnog logaritma pomicanjem na novu bazu:

[Natpis za sliku]

Osnovni logaritamski identitet

Često je u procesu rješavanja potrebno predstaviti broj kao logaritam na datu bazu. U ovom slučaju pomoći će nam sljedeće formule:

U prvom slučaju broj n postaje indikator stepena statusa u argumentu. Broj n može biti apsolutno bilo šta, jer je to samo logaritamska vrijednost.

Druga formula je zapravo parafrazirana definicija. To se zove: osnovni logaritamski identitet.

U stvari, šta će se dogoditi ako broj b podići na takav stepen da broj b ovoj potenciji daje broj a? Tako je: dobijate isti broj a. Pažljivo pročitajte ovaj odlomak ponovo - mnogi ljudi zaglave u njemu.

Kao i formule za prelazak na novu bazu, osnovni logaritamski identitet je ponekad jedino moguće rješenje.

Zadatak. Pronađite značenje izraza:

[Natpis za sliku]

Imajte na umu da je log 25 64 = log 5 8 - jednostavno uzeo kvadrat iz baze i argumenta logaritma. Uzimajući u obzir pravila za množenje potencija sa istom osnovom, dobijamo:

[Natpis za sliku]

Ako neko ne zna, ovo je bio pravi zadatak sa Jedinstvenog državnog ispita :)

Logaritamska jedinica i logaritamska nula

U zaključku ću dati dva identiteta koja se teško mogu nazvati svojstvima – radije su to posljedice definicije logaritma. Stalno se pojavljuju u problemima i, iznenađujuće, stvaraju probleme čak i „naprednim“ učenicima.

1. log a a= 1 je logaritamska jedinica. Zapamtite jednom za svagda: logaritam na bilo koju bazu a iz same ove baze jednak je jedan.
2. log a 1 = 0 je logaritamska nula. Baza a može biti bilo šta, ali ako argument sadrži jedan, logaritam je jednak nuli! Jer a 0 = 1 je direktna posljedica definicije.

To je sva imovina. Obavezno vježbajte u njihovoj primjeni! Preuzmite cheat sheet na početku lekcije, odštampajte ga i riješite probleme.

Kao što znate, kada se množe izrazi sa stepenom, njihovi eksponenti se uvijek sabiraju (a b *a c = a b+c). Ovaj matematički zakon je izveo Arhimed, a kasnije, u 8. veku, matematičar Virasen je napravio tabelu celobrojnih eksponenata. Oni su bili ti koji su služili dalje otvaranje logaritmi. Primjeri korištenja ove funkcije mogu se naći gotovo svugdje gdje trebate pojednostaviti glomazno množenje jednostavnim sabiranjem. Ako odvojite 10 minuta čitajući ovaj članak, objasnit ćemo vam što su logaritmi i kako s njima raditi. Jednostavnim i pristupačnim jezikom.

Definicija u matematici

Logaritam je izraz sljedećeg oblika: log a b=c, to jest, logaritam bilo kojeg nenegativnog broja (tj. bilo kojeg pozitivnog) “b” na njegovu bazu “a” smatra se stepenom “c ” na koju se baza “a” mora podići da bi se na kraju dobila vrijednost “b”. Analizirajmo logaritam na primjerima, recimo da postoji izraz log 2 8. Kako pronaći odgovor? Vrlo je jednostavno, potrebno je pronaći takvu snagu da od 2 do tražene snage dobijete 8. Nakon nekih proračuna u glavi, dobijamo broj 3! I to je tačno, jer 2 na stepen od 3 daje odgovor kao 8.

Vrste logaritama

Za mnoge učenike i studente ova se tema čini komplikovanom i nerazumljivom, ali zapravo logaritmi nisu toliko strašni, najvažnije je razumjeti njihovo općenito značenje i zapamtiti njihova svojstva i neka pravila. Ima ih tri pojedinačne vrste logaritamski izrazi:

1. Prirodni logaritam ln a, gdje je baza Ojlerov broj (e = 2,7).
2. Decimala a, gdje je osnova 10.
3. Logaritam bilo kojeg broja b na osnovu a>1.

Svaki od njih se rješava na standardni način, uključujući pojednostavljenje, redukciju i naknadno svođenje na jedan logaritam korištenjem logaritamskih teorema. Da biste dobili ispravne vrijednosti logaritama, trebali biste zapamtiti njihova svojstva i redoslijed radnji prilikom njihovog rješavanja.

Pravila i neka ograničenja

U matematici postoji nekoliko pravila-ograničenja koja su prihvaćena kao aksiom, odnosno nisu predmet rasprave i predstavljaju istinu. Na primjer, nemoguće je podijeliti brojeve sa nulom, a također je nemoguće izdvojiti paran korijen negativnih brojeva. Logaritmi također imaju svoja pravila, slijedeći koja možete lako naučiti raditi čak i sa dugim i prostranim logaritamskim izrazima:

• Osnova “a” uvijek mora biti veća od nule, a ne jednaka 1, inače će izraz izgubiti svoje značenje, jer su “1” i “0” u bilo kom stepenu uvijek jednaki njihovim vrijednostima;
• ako je a > 0, onda a b > 0, ispada da “c” takođe mora biti veće od nule.

Kako riješiti logaritme?

Na primjer, daje se zadatak pronaći odgovor na jednadžbu 10 x = 100. Ovo je vrlo lako, potrebno je odabrati stepen podizanjem broja deset na koji dobijamo 100. Ovo je, naravno, 10 2 = 100.

Sada predstavimo ovaj izraz u logaritamskom obliku. Dobijamo log 10 100 = 2. Prilikom rješavanja logaritma, sve radnje se praktično konvergiraju da bi se pronašla potencija na koju je potrebno unijeti bazu logaritma da bi se dobio dati broj.

Da biste precizno odredili vrijednost nepoznatog stepena, morate naučiti kako raditi s tablicom stupnjeva. izgleda ovako:

Kao što vidite, neki eksponenti se mogu pogoditi intuitivno ako imate tehnički um i poznavanje tablice množenja. Međutim, za veće vrijednosti trebat će vam stol za napajanje. Mogu ga koristiti čak i oni koji ne znaju ništa o kompleksima matematičke teme. Lijeva kolona sadrži brojeve (baza a), gornji red brojevi je vrijednost stepena c na koji je broj a podignut. Na raskrsnici ćelije sadrže brojčane vrijednosti koje su odgovor (a c =b). Uzmimo, na primjer, prvu ćeliju sa brojem 10 i kvadriramo je, dobićemo vrijednost 100, koja je naznačena na sjecištu naše dvije ćelije. Sve je tako jednostavno i lako da će i najistinskiji humanista razumjeti!

Jednačine i nejednačine

Ispada da je pod određenim uslovima eksponent logaritam. Stoga se bilo koji matematički numerički izrazi može zapisati kao logaritamska jednakost. Na primjer, 3 4 =81 se može napisati kao logaritam 81 na bazi 3 jednak četiri (log 3 81 = 4). Za negativne moći pravila su ista: 2 -5 = 1/32 zapisujemo to kao logaritam, dobijamo log 2 (1/32) = -5. Jedna od najfascinantnijih sekcija matematike je tema "logaritma". U nastavku ćemo pogledati primjere i rješenja jednadžbi, odmah nakon proučavanja njihovih svojstava. Pogledajmo sada kako izgledaju nejednakosti i kako ih razlikovati od jednačina.

Dat je izraz sljedećeg oblika: log 2 (x-1) > 3 - jeste logaritamska nejednakost, pošto je nepoznata vrijednost "x" pod znakom logaritma. I također se u izrazu upoređuju dvije veličine: logaritam željenog broja na osnovu dva je veći od broja tri.

Najvažnija razlika između logaritamskih jednadžbi i nejednačina je u tome što jednadžbe sa logaritmima (na primjer, logaritam 2 x = √9) podrazumijevaju jednu ili više specifičnih brojčanih vrijednosti u odgovoru, dok se pri rješavanju nejednadžbe uzimaju i raspon prihvatljivih vrijednosti ​​i tačke se određuju kršenjem ove funkcije. Kao posljedica toga, odgovor nije jednostavan skup pojedinačnih brojeva, kao u odgovoru na jednadžbu, već kontinuirani niz ili skup brojeva.

Osnovne teoreme o logaritmima

Prilikom rješavanja primitivnih zadataka pronalaženja vrijednosti logaritma, njegova svojstva možda neće biti poznata. Međutim, kada su u pitanju logaritamske jednačine ili nejednačine, prije svega, potrebno je jasno razumjeti i primijeniti u praksi sva osnovna svojstva logaritama. Kasnije ćemo pogledati primjere jednadžbi;

1. Glavni identitet izgleda ovako: a logaB =B. Primjenjuje se samo kada je a veće od 0, nije jednako jedan, a B je veće od nule.
2. Logaritam proizvoda može se predstaviti u sljedećoj formuli: log d (s 1 * s 2) = log d s 1 + log d s 2. U ovom slučaju preduslov je: d, s 1 i s 2 > 0; a≠1. Možete dati dokaz za ovu logaritamsku formulu, sa primjerima i rješenjem. Neka log a s 1 = f 1 i log a s 2 = f 2, tada a f1 = s 1, a f2 = s 2. Dobijamo da je s 1 * s 2 = a f1 *a f2 = a f1+f2 (osobine stepeni ), a zatim po definiciji: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, što je trebalo dokazati.
3. Logaritam količnika izgleda ovako: log a (s 1/s 2) = log a s 1 - log a s 2.
4. Teorema u obliku formule ima sljedeći oblik: log a q b n = n/q log a b.

Ova formula se naziva “svojstvo stepena logaritma”. Podsjeća na svojstva običnih stupnjeva, i nije iznenađujuće, jer se sva matematika zasniva na prirodnim postulatima. Pogledajmo dokaz.

Neka log a b = t, ispada da je a t = b. Ako oba dijela podignemo na stepen m: a tn = b n ;

ali pošto je a tn = (a q) nt/q = b n, dakle log a q b n = (n*t)/t, onda log a q b n = n/q log a b. Teorema je dokazana.

Primjeri problema i nejednakosti

Najčešći tipovi zadataka o logaritmima su primjeri jednačina i nejednačina. Nalaze se u gotovo svim knjigama zadataka, a također su obavezan dio ispita iz matematike. Za upis na fakultet ili polaganje prijemni ispiti u matematici morate znati kako pravilno rješavati takve probleme.

Nažalost, ne postoji jedinstveni plan ili shema za rješavanje i određivanje nepoznate vrijednosti logaritma, ali se može primijeniti na svaku matematičku nejednačinu ili logaritamsku jednačinu određena pravila. Prije svega, trebali biste saznati da li se izraz može pojednostaviti ili do njega dovesti opšti izgled. Duge logaritamske izraze možete pojednostaviti ako pravilno koristite njihova svojstva. Hajde da ih brzo upoznamo.

Prilikom rješavanja logaritamskih jednadžbi moramo odrediti koji tip logaritma imamo: primjer izraza može sadržavati prirodni logaritam ili decimalni.

Evo primjera ln100, ln1026. Njihovo rješenje se svodi na činjenicu da treba odrediti snagu kojoj će baza 10 biti jednaka 100 i 1026, respektivno. Za rješenja prirodnih logaritama potrebno je primijeniti logaritamski identiteti ili njihove imovine. Pogledajmo rješenje na primjerima logaritamski problemi različite vrste.

Kako koristiti logaritamske formule: s primjerima i rješenjima

Dakle, pogledajmo primjere korištenja osnovnih teorema o logaritmima.

1. Svojstvo logaritma proizvoda može se koristiti u zadacima gdje je potrebno proširiti veliki značaj brojeve b u jednostavnije činioce. Na primjer, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odgovor je 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kao što vidite, koristeći četvrto svojstvo stepena logaritma, uspjeli smo riješiti naizgled složen i nerješiv izraz. Vi samo trebate faktorisati bazu, a zatim izvući vrijednosti eksponenta iz predznaka logaritma.

Zadaci sa Jedinstvenog državnog ispita

Logaritmi se često nalaze na prijemnim ispitima, posebno mnogi logaritamski problemi na Jedinstvenom državnom ispitu (državni ispit za sve maturante). Obično su ovi zadaci prisutni ne samo u dijelu A (najlakši dio ispita), već i u dijelu C (najsloženiji i najobimniji zadaci). Ispit zahtijeva tačno i savršeno poznavanje teme „Prirodni logaritmi“.

Primjeri i rješenja problema preuzeti su od zvaničnika Opcije objedinjenog državnog ispita. Pogledajmo kako se takvi zadaci rješavaju.

Dat log 2 (2x-1) = 4. Rješenje:
prepišimo izraz, pojednostavljujući ga malo log 2 (2x-1) = 2 2, po definiciji logaritma dobijamo da je 2x-1 = 2 4, dakle 2x = 17; x = 8,5.

• Najbolje je sve logaritme svesti na istu bazu kako rješenje ne bi bilo glomazno i ​​zbunjujuće.
• Svi izrazi pod predznakom logaritma su označeni kao pozitivni, stoga, kada se eksponent izraza koji je pod predznakom logaritma i kao njegova baza izvadi kao množitelj, izraz koji ostaje pod logaritmom mora biti pozitivan.