मैं संक्षिप्त रहूंगा। दो सीधे के बीच कोण उनके गाइड वैक्टर के बीच कोने के बराबर है। इस प्रकार, यदि आप गाइड वैक्टर के निर्देशांक को ढूंढते हैं तो \u003d (x 1; y 1; z 1) और b \u003d (x 2; y 2; z 2), तो आप एक कोण पा सकते हैं। अधिक सटीक रूप से, सूत्र द्वारा कोने की कोसाइन:

आइए देखें कि यह सूत्र विशिष्ट उदाहरणों पर कैसे काम करता है:

एक कार्य। क्यूबा एबीसीडीए 1 बी 1 सी 1 डी 1 में, अंक ई और एफ क्रमशः 1 बी 1 और बी 1 सी 1 पसलियों के बीच हैं। सीधे एई और बीएफ के बीच कोण खोजें।

चूंकि क्यूब के किनारे निर्दिष्ट नहीं है, हमने एबी \u003d 1. हम एक मानक समन्वय प्रणाली पेश करते हैं: बिंदु ए, एक्स, वाई अक्ष पर प्रारंभ करें, क्रमशः एबी, विज्ञापन और एए 1 के साथ भेजें। एक एकल सेगमेंट एबी \u003d 1. अब हम अपनी सीधी रेखाओं के लिए गाइड वैक्टर के निर्देशांक पाते हैं।

हम एई वेक्टर के निर्देशांक पाएंगे। इसके लिए, हमें अंक की आवश्यकता होगी \u003d (0; 0; 0) और e \u003d (0.5; 0; 1)। चूंकि बिंदु ई सेगमेंट के बीच में 1 बी 1 है, इसके निर्देशांक अंत के औसत अंकगणितीय निर्देशांक के बराबर हैं। ध्यान दें कि वेक्टर एई की शुरुआत निर्देशांक की शुरुआत के साथ मेल खाती है, इसलिए एई \u003d (0.5; 0; 1)।

अब हम बीएफ वेक्टर से निपटेंगे। इसी तरह, हम अंक b \u003d (1; 0; 0) और f \u003d (1; 0.5; 1) को अलग करते हैं, क्योंकि एफ - सेगमेंट के बीच बी 1 सी 1। हमारे पास है:
Bf \u003d (1 - 1; 0.5 - 0; 1 - 0) \u003d (0; 0.5; 1)।

तो, गाइड वैक्टर तैयार हैं। सीधे के बीच कोण का कोसाइन गाइड वैक्टर के बीच कोण का कोसाइन है, इसलिए हमारे पास है:

एक कार्य। एबीसीए 1 बी 1 सी 1 के सही ट्रिकोरल प्रिज्म में, जिनमें से सभी पसलियां 1 हैं, अंक डी और ई क्रमशः 1 बी 1 और बी 1 सी 1 पसलियों के बीच को चिह्नित करते हैं। सीधे विज्ञापन और होने के बीच कोण का पता लगाएं।

हम मानक समन्वय प्रणाली का परिचय देते हैं: बिंदु ए पर मूल, एक्स अक्ष एए 1 के साथ एबी, जेड के साथ निर्देशित करेगा। वाई अक्ष भेजेगा ताकि ऑक्सी विमान एबीसी विमान के साथ मेल खाता हो। एक एकल सेगमेंट एबी \u003d 1. वांछित प्रत्यक्ष के लिए गाइड वैक्टर के निर्देशांक का पता लगाएं।

शुरू करने के लिए, हम विज्ञापन वेक्टर के निर्देशांक पाएंगे। अंक पर विचार करें: ए \u003d (0; 0; 0) और डी \u003d (0.5; 0; 1), क्योंकि D सेगमेंट के बीच में 1 बी 1 है। चूंकि विज्ञापन वेक्टर की शुरुआत निर्देशांक की उत्पत्ति के साथ मेल खाती है, इसलिए हम विज्ञापन \u003d (0.5; 0; 1) प्राप्त करते हैं।

अब हमें वेक्टर के निर्देशांक मिलते हैं। बिंदु बी \u003d (1; 0; 0) इसे आसान माना जाता है। बिंदु ई के साथ - सेगमेंट के बीच सी 1 बी 1 - थोड़ा और जटिल। हमारे पास है:

यह एक कोसाइन कोण खोजने के लिए बनी हुई है:

एक कार्य। सही हेक्सागोन पुरस्कार में abcdefa 1 बी 1 डी 1 डी 1 ई 1 एफ 1, जिनके सभी किनारों 1 हैं, अंक k और l क्रमशः 1 बी 1 और बी 1 सी 1 पसलियों के बीच हैं। सीधे एके और बीएल के बीच कोण खोजें।

हम प्रिज्म के लिए मानक समन्वय प्रणाली का परिचय देते हैं: निर्देशांक की शुरुआत निचले आधार के केंद्र में रखी जाएगी, एक्स अक्ष एफसी के साथ निर्देशित करेगी, एक्सिस वाई - एबी और डी के सेगमेंट के बीच के माध्यम से, और जेड अक्ष लंबवत है। एक भी कट फिर से एबी \u003d 1 के बराबर है: हम रुचि के निर्देशांक को लिखेंगे:

अंक k और l क्रमशः 1 बी 1 और बी 1 सी 1 सेगमेंट के बीच हैं, इसलिए उनके निर्देशांक अंकगणितीय औसत के माध्यम से हैं। जानने के अंक, हम गाइड वैक्टर के निर्देशांक एके और बीएल:

अब हम कोने की कोसाइन पाते हैं:

एक कार्य। सही चतुर्भुज sabcd पिरामिड में, जिनमें से सभी पसलियों 1 हैं, अंक ई और एफ क्रमशः एसबी और एससी के किनारे हैं। सीधे एई और बीएफ के बीच कोण खोजें।

हम एक मानक समन्वय प्रणाली पेश करते हैं: बिंदु ए पर प्रारंभ करें, x और y अक्ष क्रमशः एबी और एडी के साथ भेजे जाएंगे, और जेड अक्ष लंबवत रूप से निर्देशित होंगे। एक एकल खंड ab \u003d 1 है।

अंक ई और एफ - एसबी और एससी सेगमेंट की माडिंग्स क्रमशः, इसलिए उनके निर्देशांक अंत के अंकगणितीय औसत के रूप में स्थित हैं। हम अपने लिए ब्याज के निर्देशांक लिखते हैं:
A \u003d (0; 0; 0); B \u003d (1; 0; 0)

अंक जानकर, हम मार्गदर्शिका वैक्टर एई और बीएफ के निर्देशांक पाएंगे:

एई वेक्टर के निर्देशांक बिंदु ई के निर्देशांक के साथ मेल खाते हैं, क्योंकि बिंदु ए निर्देशांक की शुरुआत है। यह एक कोसाइन कोण खोजने के लिए बनी हुई है:

गणित में सी 2 के कार्य में, यह निर्धारित करने के लिए आवश्यक कार्य को हल करने के लिए अक्सर आवश्यक होता है:

1. दो बिंदुओं के बीच की दूरी
2. बिंदु से सीधे दूरी तक
3. बिंदु से विमान की दूरी
4. क्रॉस-कंट्री के बीच की दूरी सीधे
5. दो सीधे के बीच कोण
6. सीधे और विमान के बीच कोण
7. विमानों के बीच कोण

कार्य प्राथमिक हैं, यदि आप समाधान सी 2 के एल्गोरिदम का पालन करते हैं और मूल त्रिकोणमितीय गुणों को याद करते हैं, जैसे विकर्णों के गुण या पॉलीहेड्रॉन के सतह क्षेत्र। सहायक कार्य आपको इन बुनियादी गुणों को याद करने में मदद करेंगे।

अब हम सीधे एल्गोरिदम में बदल जाते हैं।

1. दो बिंदुओं के बीच की दूरी निर्धारित करने के लिए और हम दो तरीकों में से एक का उपयोग करते हैं:

• कुछ त्रिकोण के लिए एवी को चालू करें और इसे त्रिभुज पक्ष के रूप में खोजें
• सूत्र के अनुसार

इसके अलावा, मेरी राय में समन्वय विधि सरल है, केवल प्रत्येक बिंदु के निर्देशांक को धीरे-धीरे निर्धारित करना आवश्यक है।

2. बिंदु से प्रत्यक्ष गणना तक की दूरी निर्धारित करने के लिए

• लंबवत खंड की लंबाई की तरह, यदि इस सेगमेंट को कुछ त्रिभुज में ऊंचाई में से एक के रूप में चालू करना संभव है

उस क्षेत्र की गणना के लिए सूत्र का उपयोग करके समन्वय विधि का उपयोग करना जिसमें वांछित दूरी ऊंचाई होगी और

3. बिंदु से विमान तक की दूरी बराबर है

• लंबवत की लंबाई, इस बिंदु से विमान तक कम हो गई। ऐसा करने के लिए, ध्यान से हम एक क्रॉस सेक्शन का निर्माण करते हैं, जो विमान के लिए लंबवत है और एक निर्दिष्ट बिंदु के माध्यम से गुजरता है। वांछित दूरी परिणामस्वरूप नए पॉलीहेड्रॉन की ऊंचाई के बराबर होगी।
• समन्वय विधि का उपयोग करना

समीकरण इस विमान से संबंधित तीन बिंदुओं के निर्देशांकों को बदलकर है

• एक वेक्टर विधि का उपयोग करना

ऐसा करने के लिए, हमें वैक्टर के अतिरिक्त और घटाव के नियमों को याद रखना चाहिए कि लंबवत वैक्टर का उत्पाद शून्य है।

• वॉल्यूम विधि द्वारा, यदि एवीएसएम का एक पिरामिड है, तो एबीसी त्रिभुज युक्त विमान के बिंदु मीटर से दूरी सूत्र द्वारा गणना की जाती है

• सहायक कार्यों का तरीका जिसे देखा जा सकता है

4. क्रॉसिंग डायरेक्ट के बीच की दूरी को हल किया जा सकता है

4.1। चरणबद्ध और कम्प्यूटेशनल विधि:

• दो क्रॉस-लाइनों के लिए एक सामान्य लंबवत बनाएं और इसे लंबाई ढूंढें;
• एक विमान का निर्माण सीधे और समानांतर दूसरे में से एक है। फिर वांछित दूरी बिंदु से दूरी के बराबर होगी जो विमान में बनाई गई सीधी रेखा तक होगी;
• निष्कर्ष सीधे डेटा पार करने के समानांतर विमानों में प्रत्यक्ष डेटा, इन विमानों के बीच की दूरी को ढूंढें
• इनमें से किसी एक के लिए एक विमान लंबवत बनाएं और दूसरे प्रत्यक्ष के ऑर्थोगोनल प्रक्षेपण का निर्माण करें

4.2। वेक्टर-समन्वय विधि

• हमें सेगमेंट के सिरों के निर्देशांक मिलते हैं, जो दो क्रॉस-लाइव सीधी रेखाओं का एक आम लंबवत है
• दो बिंदुओं के बीच की दूरी का पता लगाएं

4.3। वेक्टर विधि
यह कार्य उस लंबवत से संबंधित वेक्टर की लंबाई निर्धारित करना है जिसमें से दो क्रॉस-लाइक सीधी रेखाओं का एक आम लंबवत है।

6. सीधे और विमान के बीच कोणयह इसे एक आयताकार त्रिभुज में एक तेज कोनों, या एक वेक्टर समन्वयक विधि के रूप में शामिल करके निर्धारित किया जाता है।

चूंकि कोण विमानों के बीच निर्धारित होता है, अगले पाठ में विचार करें। समाधान के ये एल्गोरिदम सी 2 कार्य को हल करने की विधि की व्यापक समझ में योगदान देते हैं। "स्कूली बच्चों और उनके माता-पिता के लिए छात्र पत्रिका की मदद करने के लिए।" और पढ़ें: http://education-club.ru/#ixzz2ixf5googleju

7. विमानों के बीच कोण(ज्यामितीय विधि)

• 1. जिस पर विमान को छेड़छाड़ की जाती है उसे डायरेक्ट करें।
• 2. इस प्रत्यक्ष बिंदु पर चुनें और इन विमानों में झूठ बोलने के लिए दो लंबवत ले जाएं। या विमानों की क्रॉसिंग लाइन के लिए लंबवत एक विमान ले जाएं।
• 3. विमानों के रेखा चौराहे के लिए लंबवत द्वारा गठित कोण के त्रिकोणमितीय फ़ंक्शन का पता लगाएं। एक नियम के रूप में, हम इसे त्रिभुज के माध्यम से करते हैं, जिसमें वांछित कोण शामिल है।
• 4. कोण के मूल्य, या कोण के त्रिकोणमितीय कार्य को लिखने के जवाब में।

विमानों के बीच कोण। समन्वय विधि। कार्य सी 2।

दो इंटरसेक्टिंग विमान एक दूसरे के डमी कोनों के दो जोड़े बनाते हैं:

द्वारबोन कोण की परिमाण संबंधित रैखिक कोण के मूल्य से मापा जाता है।

एक द्वारफ्रानी कोने के एक रैखिक कोण का निर्माण करने के लिए, आपको लाइन चौराहे रेखाओं पर एक मनमानी बिंदु लेने की आवश्यकता है, और प्रत्येक विमान में विमानों की रेखा चौराहे के लिए लंबवत एक बीम ले जाने के लिए। इन किरणों द्वारा बनाई गई कोण डिहाइड्रल कोण का रैखिक कोण है:

विमानों के बीच कोण का मूल्य कम से कम घुमावदार कोण की परिमाण है।

हमारे विमानों को दें और समीकरणों द्वारा निर्धारित किए गए हैं:

विमानों के बीच कोने की कोसाइन इस तरह के सूत्र में है:

जवाब में, हम रिकॉर्ड करते हैं, क्योंकि विमानों के बीच कोण का मूल्य एक छोटे से गर्भपात की परिमाण है।

दाहिने चतुर्भुज प्रिज्म में आधार पर आधार 12 और ऊंचाई 21 का आधार बिंदु एम को लिया गया है। किनारे को प्वाइंट के लिए लिया जाता है। विमान और विमान के बीच कोण का पता लगाएं।

एक ड्राइंग बनाओ। चूंकि हम समन्वय विधि का उपयोग करेंगे, तुरंत समन्वय प्रणाली को पेश करेंगे: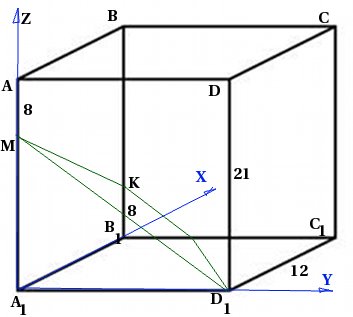

अब हमारे पास विमान और विमान के समीकरणों को लिखने का कार्य है।

मैंने वर्णित तीन बिंदुओं के लिए विमान के समीकरण को खोजने के लिए एक विस्तृत एल्गोरिदम।

विमान और विमान के समीकरणों में गुणांक खोजने के बाद, हम उन्हें विमानों के बीच कोण को कोण खोजने के लिए सूत्र में प्रतिस्थापित करते हैं, और कोण ढूंढते हैं।

मैं आपको इस कार्य का एक विस्तृत वीडियो देखने का सुझाव देता हूं:

Inna Vladimirovna Feldman का एक और कार्य

वीडियो सबक "समन्वय विधि समाधान समाधान सी -2"

पाठ 2 http://youtu.be/dkqwg8ozrgo।
पाठ 3 http://youtu.be/ddgr0pnbfno।
पाठ 4 http://youtu.be/n6yx2pqc0lo
पाठ 5 http://youtu.be/jkwbxaw1yli।
पाठ 6 http://youtu.be/gybickcmkbii।
पाठ 7 http://youtu.be/_lparpyxp5g।
पाठ 8 http://youtu.be/xjhyzqoofd8।

इस आलेख में, ईई से सी 2 समस्या को हल करने के उदाहरण पर, समन्वय विधि का उपयोग करके एक विधि को अलग किया जाता है। याद रखें कि सीधी रेखाएं पार हो रही हैं, अगर वे एक ही विमान में झूठ नहीं बोल रहे हैं। विशेष रूप से, यदि कोई विमान विमान में स्थित है, और दूसरा प्रत्यक्ष इस विमान को उस बिंदु पर पार करता है जो पहली सीधी रेखा पर झूठ नहीं बोलता है, तो ऐसी सीधी रेखाएं पार कर रही हैं (आंकड़े देखें)।

ढूँढ़ने के लिए क्रॉस-कंट्री के बीच की दूरी सीधे जरुरत:

1. क्रॉस-ऑन डायरेक्ट प्लेन में से एक के माध्यम से आचरण, जो एक और क्रॉस-मूविंग सीधी रेखा के समानांतर है।
2. परिणामस्वरूप विमान के किसी भी बिंदु के किसी भी बिंदु से कम लंबवत। इस लंबवत की लंबाई सीधे के बीच वांछित दूरी होगी।

हम गणित ईई से सी 2 समस्या को हल करने के उदाहरण पर इस एल्गोरिदम का अधिक विस्तार से विश्लेषण करेंगे।

अंतरिक्ष में सीधे दूरी

एक कार्य। एकल घन में एबीसीडीए। 1 बी 1 सी। 1 डी 1 सीधे के बीच की दूरी का पता लगाएं बी 0 ए। 1 I डाटाबेस 1 .

अंजीर। 1. कार्य के लिए ड्राइंग

फेसला। विकर्ण घन के बीच के माध्यम से डाटाबेस 1 (बिंदु) ओ) हम प्रत्यक्ष, समानांतर प्रत्यक्ष खर्च करेंगे ए। 1 बी। पसलियों के साथ इस लाइन के चौराहे का बिंदु बीसी। तथा ए। 1 डी 1 तदनुसार इंगित करें एन तथा म।। सीधे एमएन। विमान में झूठ एमएनबी। 1 और प्रत्यक्ष के समानांतर ए। 1 बीजो इस विमान में झूठ नहीं बोलता है। इसका मतलब है कि सीधे ए। 1 बी समानांतर विमान एमएनबी। 1 सीधे और विमान (चित्र 2) के समानांतरता के आधार पर।

अंजीर। 2. क्रॉस-मूविंग स्ट्रेट के बीच वांछित दूरी चयनित प्रत्यक्ष के किसी भी बिंदु से दूरी के बराबर है

हम कुछ बिंदु प्रत्यक्ष से दूरी की तलाश कर रहे हैं ए। 1 बी विमान के लिए एमएनबी। एक । परिभाषा के अनुसार यह दूरी सीधे क्रॉस-कंट्री के बीच वांछित दूरी होगी।

इस दूरी को खोजने के लिए, हम समन्वय विधि का उपयोग करते हैं। हम एक आयताकार कार्टेशियन समन्वय प्रणाली पेश करते हैं ताकि इसकी शुरुआत बिंदु बी, अक्ष के साथ मेल खाती हो एक्स। किनारे के साथ निर्देशित किया गया था बी 0 ए।, एक्सिस वाई - पसलियों के साथ बीसी।, एक्सिस जेड - पसलियों के साथ बी.बी. 1 (चित्र 3)।

अंजीर। 3. आयताकार कार्टेशियन समन्वय प्रणाली आकृति में दिखाए गए अनुसार चुनें

विमान के समीकरण का पता लगाएं एमएनबी। 1 इस समन्वय प्रणाली में। ऐसा करने के लिए, बिंदुओं के पहले निर्देशांक निर्धारित करें म।, एन तथा बी 1: परिणामस्वरूप समन्वय सामान्य समीकरण प्रत्यक्ष में विकल्प और हम समीकरणों की निम्नलिखित प्रणाली प्राप्त करते हैं:

सिस्टम के दूसरे समीकरण से, हम तीसरे से प्राप्त करते हैं जिसके बाद हम पहले से ही सामान्य समीकरण प्रत्यक्ष रूप से प्राप्त मूल्यों को प्रतिस्थापित करते हैं:

हम देखते हैं कि अन्यथा विमान एमएनबी। 1 निर्देशांक की उत्पत्ति के माध्यम से होगा। हम इस समीकरण के दोनों हिस्सों को विभाजित करते हैं और प्राप्त करते हैं:

बिंदु से विमान तक की दूरी सूत्र द्वारा निर्धारित की जाती है।

समन्वय विधि अंतरिक्ष में स्टीरियोमीटर वस्तुओं के बीच किसी भी कोण या दूरी को खोजने का एक बहुत ही कुशल और सार्वभौमिक विधि है। यदि गणित में आपके शिक्षक की उच्च योग्यताएं हैं, तो उसे यह पता होना चाहिए। अन्यथा, मैं आपको "के साथ" भाग के लिए ट्यूटर बदलने की सलाह दूंगा। गणित में ईजीई की तैयारी सी 1-सी 6 में आमतौर पर नीचे वर्णित मुख्य एल्गोरिदम और सूत्रों का विश्लेषण शामिल है।

सीधे ए और बी के बीच कोण

अंतरिक्ष में प्रत्यक्ष के बीच कोण को सीधे उन्हें छेड़छाड़ करने के लिए कोण कहा जाता है। यह कोण प्रत्यक्ष डेटा के गाइड वैक्टर (या 180 डिग्री तक पूरक) के बीच कोने के बराबर है।

कोण की खोज के लिए क्या एल्गोरिदम गणित ट्यूटर का उपयोग करता है?

1) किसी भी वेक्टर को चुनें और प्रत्यक्ष ए और बी (उनके समानांतर) के निर्देश हैं।
2) वैक्टर के निर्देशांक का निर्धारण करें और उनके प्रासंगिक निर्देशांकों को शुरू करें और समाप्त हो जाएं (वेक्टर के अंत के समन्वय से आपको शुरुआत निर्देशांक लेने की आवश्यकता है)।
3) हम सूत्र में पाए गए निर्देशांक को प्रतिस्थापित करते हैं:
। कोने को खोजने के लिए, आपको परिणाम की arquosine खोजने की जरूरत है।

विमान के लिए सामान्य

विमान के लिए सामान्य को इस विमान के लिए लंबवत किसी भी वेक्टर कहा जाता है।
सामान्य कैसे खोजें? सामान्य के निर्देशांक की खोज करने के लिए, यह इस विमान में झूठ बोलने वाले किसी भी तीन बिंदु मीटर, एन और के निर्देशांक को जानने के लिए पर्याप्त है। इन निर्देशांक के अनुसार, हम वैक्टर के निर्देशांक पाते हैं और और शर्तों की पूर्ति की आवश्यकता होती है। शून्य पर वैक्टर के स्केलर उत्पाद को समान रूप से, हम तीन चर के साथ समीकरणों की एक प्रणाली बनाते हैं, जिससे आप सामान्य के निर्देशांक पा सकते हैं।

गणित ट्यूटर : सिस्टम को पूरी तरह से हल करना आवश्यक नहीं है, क्योंकि यह कम से कम एक सामान्य चुनने के लिए पर्याप्त है। ऐसा करने के लिए, इसके किसी भी अज्ञात निर्देशांक (उदाहरण के लिए, एक इकाई) में से किसी एक को प्रतिस्थापित करना संभव है और शेष दो अज्ञात के साथ दो समीकरणों की प्रणाली को हल करना संभव है। यदि इसमें समाधान नहीं हैं, तो इसका मतलब है कि सामान्य परिवार में कोई भी नहीं है कि इकाई चयनित चर के लिए इसके लायक है। फिर किसी अन्य चर (अन्य निर्देशांक) की बजाय इकाई को प्रतिस्थापित करें और नई प्रणाली का फैसला करें। यदि आप फिर से चूकते हैं, तो आपके सामान्य के पास अंतिम समन्वय के अनुसार एक इकाई होगी, और यह किसी प्रकार के समन्वय विमान के समानांतर होगा (इस मामले में सिस्टम के बिना इसे ढूंढना आसान है)।

मान लीजिए कि हमें मार्गदर्शिका वेक्टर और सामान्य के निर्देशांक का एक सीधा और विमान दिया जाता है
सीधे और विमान के बीच कोण निम्नलिखित सूत्र द्वारा गणना की जाती है:

इन विमानों के लिए दोनों दो सामान्य हैं। फिर विमानों के बीच कोण की कोसाइन मानदंडों के बीच कोण के कोसाइन के मॉड्यूल के बराबर है:

अंतरिक्ष में विमान समीकरण

अंक जो समानता को संतुष्ट करते हैं, एक सामान्य के साथ एक विमान बनाते हैं। गुणांक एक ही निर्दिष्ट सामान्य के साथ दो विमानों के बीच विचलन (समांतर शिफ्ट) की परिमाण के लिए ज़िम्मेदार है। विमान समीकरण लिखने के लिए, आपको पहले अपने सामान्य (जैसा कि ऊपर वर्णित वर्णित) को ढूंढना होगा, और फिर विमान के किसी भी बिंदु के समन्वय को सामान्य सामान्य के निर्देशांक के साथ समीकरण के समन्वय के साथ प्रतिस्थापित करना होगा और गुणांक ढूंढें।

प्रथम स्तर

निर्देशांक और वैक्टर। संपूर्ण गाइड (2019)

इस लेख में, हम एक "चॉपस्टिस स्टिक" की चर्चा शुरू करेंगे, जो आपको सरल अंकगणित के लिए कई ज्यामिति कार्यों को कम करने की अनुमति देगा। यह "छड़ी" आपके जीवन को विशेष रूप से इस मामले में काफी कम कर सकती है जब आप स्थानिक आंकड़ों, वर्गों आदि के निर्माण में असाधारण महसूस करते हैं। इन सभी को एक निश्चित कल्पना और व्यावहारिक कौशल की आवश्यकता होती है। विधि, जिसे हम यहां पर विचार करना शुरू कर देंगे, आपको सभी प्रकार के ज्यामितीय निर्माण और तर्क से लगभग पूरी तरह से सार करने की अनुमति देंगे। विधि कहा जाता है "समन्वय विधि"। इस लेख में, हम निम्नलिखित प्रश्नों पर विचार करेंगे:

1. विमान का समन्वय
2. विमान पर अंक और वैक्टर
3. दो बिंदुओं के साथ एक वेक्टर का निर्माण
4. वेक्टर की लंबाई (दो बिंदुओं के बीच की दूरी)
5. कट के बीच के निर्देशांक
6. स्केलर उत्पाद वैक्टर
7. दो वैक्टर के बीच कोने

मुझे लगता है कि आपने पहले ही अनुमान लगाया है कि समन्वय विधि को क्यों कहा जाता है? सच है, इसे ऐसा नाम प्राप्त हुआ, क्योंकि यह ज्यामितीय वस्तुओं के साथ नहीं संचालित होता है, बल्कि उनकी संख्यात्मक विशेषताओं (निर्देशांक) के साथ। और रूपांतरण स्वयं, जो आपको ज्यामिति से बीजगणित तक जाने की अनुमति देता है, समन्वय प्रणाली को पेश करना है। यदि स्रोत आकृति फ्लैट थी, तो निर्देशांक द्वि-आयामी होते हैं, और यदि गठन आकृति होती है, तो निर्देशांक त्रि-आयामी होते हैं। इस लेख में हम केवल दो-आयामी मामले पर विचार करेंगे। और लेख का मुख्य उद्देश्य आपको समन्वय विधि की कुछ बुनियादी तकनीकों का उपयोग करने के लिए सिखाना है (वे कभी-कभी उपयोग भाग बी में योजनाओं में समस्याओं को हल करने में उपयोगी होते हैं)। इस विषय पर निम्नलिखित दो खंड कार्य सी 2 (स्टीरियोमेट्री के लिए कार्य) की समस्याओं को हल करने के लिए समान तरीकों पर चर्चा करने के लिए समर्पित हैं।

निर्देशांक की विधि पर चर्चा शुरू करने के लिए यह तार्किक क्यों होगा? शायद, समन्वय प्रणाली की अवधारणा के साथ। याद रखें जब आप उसके साथ पहले सामना करते थे। ऐसा लगता है कि ग्रेड 7 में, जब आप एक रैखिक फ़ंक्शन के अस्तित्व के बारे में सीखा, उदाहरण के लिए। मुझे आपको याद दिलाने दें, आपने इसे अंक पर बनाया है। क्या तुम्हें याद है? आपने एक मनमानी संख्या चुनी, इसे सूत्र में प्रतिस्थापित किया और इस तरह से गणना की। उदाहरण के लिए, यदि, तो, यदि, तो, आदि, अंत में आपको क्या मिला? और मुझे निर्देशांक के साथ एक बिंदु मिला: और। इसके बाद, आपने "क्रॉस" (समन्वय प्रणाली) को चित्रित किया, इस पर एक पैमाने का चयन किया (आपके पास कितनी कोशिकाएं होंगी) और इस पर ध्यान दिया गया अंक प्राप्त हुए, जो तब सीधे लाइन, परिणामी रेखा को जोड़ते हैं और वहां हैं एक समारोह ग्राफ।

ऐसे कई क्षण हैं जिन्हें आपको थोड़ा और समझाया जाना चाहिए:

1. एक भी सेगमेंट जो आप सुविधा के लिए चुनते हैं, ताकि चित्र में सब कुछ सुंदर और कॉम्पैक्टली फिट हो

2. यह स्वीकार किया जाता है कि धुरी दाएं से बाएं हो जाती है, और धुरी नीचे की ओर है

3. वे समकोण पर छेड़छाड़ करते हैं, और उनके चौराहे के बिंदु को निर्देशांक की शुरुआत कहा जाता है। यह पत्र द्वारा इंगित किया गया है।

4. बिंदु के निर्देशांक की रिकॉर्डिंग में, उदाहरण के लिए, ब्रैकेट में बाईं ओर धुरी के साथ एक बिंदु समन्वय होता है, और दाईं ओर, धुरी के साथ। विशेष रूप से, बस इसका मतलब है कि बिंदु

5. समन्वय अक्ष पर किसी भी बिंदु को सेट करने के लिए, इसे अपने निर्देशांक (2 नंबर) निर्दिष्ट करने की आवश्यकता है

6. किसी भी बिंदु के लिए धुरी पर झूठ बोलना,

7. किसी भी बिंदु के लिए धुरी पर झूठ बोलना,

8. अक्ष को Abscissa अक्ष कहा जाता है

9. अक्ष को ऑर्डिनेट एक्सिस कहा जाता है

अब चलिए अगले चरण को आपके साथ बनाते हैं: हम दो बिंदुओं पर ध्यान देते हैं। सेगमेंट के साथ इन दो बिंदुओं को कनेक्ट करें। और तीर को डालें जैसे कि हम बिंदु से बिंदु तक एक सेगमेंट खर्च करते हैं: यानी, हम अपने सेगमेंट को निर्देशित करेंगे!

याद रखें कि निर्देशित खंड को और कैसे कहा जाता है? सच है, इसे एक वेक्टर कहा जाता है!

इस प्रकार, अगर हम एक बिंदु के साथ एक बिंदु कनेक्ट करते हैं, इसके अलावा, हमारे पास एक बिंदु ए, और अंत - बिंदु बी होगा, फिर हमें एक वेक्टर मिलता है। क्या आपने इस इमारत को ग्रेड 8 में भी किया है, याद है?

यह पता चला है कि अंक की तरह वैक्टर, दो संख्याओं से दर्शाया जा सकता है: इन संख्याओं को वेक्टर निर्देशांक कहा जाता है। प्रश्न: क्या आपको लगता है कि हमारे समन्वय को खोजने के लिए वेक्टर की शुरुआत और अंत के निर्देशांक को जानना हमारे लिए पर्याप्त है? यह पता चला है कि हाँ! और यह बहुत आसान हो गया है:

इस प्रकार, चूंकि डॉट वेक्टर शुरुआत है, और अंत, वेक्टर के पास निम्नलिखित निर्देशांक हैं:

उदाहरण के लिए, यदि, वेक्टर के निर्देशांक

अब चलो इसके विपरीत करते हैं, हम वेक्टर के निर्देशांक पाएंगे। हमें इसके लिए क्या बदलना चाहिए? हां, आपको शुरुआत और अंत को स्वैप करने की आवश्यकता है: अब वेक्टर की शुरुआत बिंदु पर होगी, और अंत बिंदु पर है। फिर:

ध्यान से देखो, वैक्टर के बीच क्या अंतर है और? उनका एकमात्र अंतर निर्देशांक में संकेत है। वे विपरीत हैं। इस तथ्य को इस तरह रिकॉर्ड करने के लिए स्वीकार किया जाता है:

कभी-कभी, यदि यह विशेष रूप से निर्धारित नहीं होता है, तो कौन सा बिंदु वेक्टर की शुरुआत है, और कैसे अंत, वैक्टर को दो पूंजी अक्षरों से दर्शाया जाता है, लेकिन एक पंक्ति, उदाहरण के लिए: आदि।

अब थोड़ा पेनट और निम्नलिखित वैक्टर के निर्देशांक को ढूंढें:

चेक:

और अब एक समस्या का निर्धारण थोड़ा और जटिल है:

इस बिंदु पर ऑन-चा-स्क्रैप के साथ एक शताब्दी में एक सह-या-डी-ऑन-आप हैं। नाई-डाइट एबीएस सीआईएसएस डीओपी।

वही सुंदर गद्य है: बिंदु के निर्देशांक को दें। फिर

मैं यह निर्धारित करने के लिए एक प्रणाली हूं कि वेक्टर के निर्देशांक क्या हैं। तब बिंदु का समन्वय होता है। हम Abscissa में रुचि रखते हैं। फिर

उत्तर:

आप वैक्टर के साथ और क्या कर सकते हैं? हां, लगभग सभी समान संख्या के समान ही (जब तक आप विभाजित नहीं हो सकते, तब तक आप दो तरीकों से गुणा करना संभव है, जिनमें से एक हम यहां थोड़ी देर बाद चर्चा करेंगे)

1. वैक्टर को एक दूसरे के साथ जोड़ा जा सकता है
2. एक दूसरे से वैक्टर काटा जा सकता है
3. वेक्टर को एक मनमाने ढंग से nonzero संख्या पर गुणा (या विभाजित) किया जा सकता है
4. वैक्टर को एक दूसरे से गुणा किया जा सकता है

इन सभी परिचालनों में एक पूरी तरह से दृश्य ज्यामितीय प्रतिनिधित्व है। उदाहरण के लिए, अतिरिक्त और घटाव के लिए त्रिभुज (या समांतरोग्राम) का एक नियम:

वेक्टर को गुणा या विभाजित करते समय दिशा को संपीड़ित या संपीड़ित या बदलता है:

हालांकि, यहां हमें निर्देशांक के साथ क्या हो रहा है के सवाल में दिलचस्पी होगी।

1. दो वैक्टरों के जोड़ने (घटाने) को जोड़ते समय, हम वैकल्पिक रूप से उनके निर्देशांक को गुना (कटौती) करते हैं। अर्थात:

2. वेक्टर के गुणा (विभाजन) को संख्या से गुणा करने पर, इसके सभी निर्देशांक इस संख्या में गुणा (विभाजित) होते हैं:

उदाहरण के लिए:

· नाय-मर-या-डीएटी की पलक का योग मरना।

आइए पहले प्रत्येक वैक्टर के निर्देशांक पाएं। उनमें से दोनों की शुरुआत - मूल का बिंदु है। उनके पास अलग-अलग सिर हैं। फिर। अब हम वेक्टर के निर्देशांक की गणना करते हैं, तो परिणामी वेक्टर के निर्देशांक का योग बराबर होता है।

उत्तर:

अब निम्नलिखित कार्य है:

· वेक्टर के निर्देशांक का योग पाएं

चेक:

आइए अब निम्नलिखित कार्य पर विचार करें: हमारे पास समन्वय विमान पर दो अंक हैं। उनके बीच की दूरी कैसे खोजें? पहले बिंदु, और दूसरा। उनके बीच की दूरी को दर्शाते हैं। आइए स्पष्टता के लिए निम्नलिखित ड्राइंग करें:

मैंने क्या किया? सबसे पहले, मैं, सबसे पहले, जुड़े अंक और, और बिंदु से रेखा, अक्ष के समानांतर, और रेखा को अक्ष के समानांतर बिंदु से बिताया। क्या वे एक अद्भुत आकृति बनाकर इस बिंदु पर पार हो गए हैं? यह क्या अद्भुत है? हां, हम लगभग आयताकार त्रिभुज के बारे में जान रहे हैं। खैर, पाइथागोरा का प्रमेय - निश्चित रूप से। वांछित खंड इस त्रिभुज का hypotenuse है, और सेगमेंट Kartets हैं। बिंदु के निर्देशांक क्या हैं? हां, उन्हें तस्वीर में ढूंढना आसान है: चूंकि सेगमेंट कुल्हाड़ियों के समानांतर हैं और तदनुसार, उनकी लंबाई ढूंढना आसान है: यदि आप क्रमशः सेगमेंट की लंबाई निर्दिष्ट करते हैं, तो

अब हम पायथागोरियन प्रमेय का उपयोग करते हैं। हम कैथेट की लंबाई जानते हैं, हम hypotenuse पाएंगे:

इस प्रकार, दो बिंदुओं के बीच की दूरी निर्देशांक से मतभेदों के वर्गों के योग की जड़ है। या - दो बिंदुओं के बीच की दूरी सेगमेंट की लंबाई है, जो उन्हें जोड़ती है। यह ध्यान देना आसान है कि अंक के बीच की दूरी दिशा पर निर्भर नहीं है। फिर:

यहां से हम तीन आउटपुट बनाते हैं:

आइए दो बिंदुओं के बीच की दूरी की गणना में थोड़ा अभ्यास करें:

उदाहरण के लिए, यदि, तो दूरी के बीच और बराबर है

या चलो अलग-अलग जाते हैं: हमें वेक्टर के निर्देशांक मिलते हैं

और वेक्टर की लंबाई पाएं:

जैसा कि आप देख सकते हैं, वही बात!

अब थोड़ा अभ्यास करें:

कार्य: निर्दिष्ट बिंदुओं के बीच की दूरी का पता लगाएं:

चेक:

यहां एक ही सूत्र पर कार्यों की एक और जोड़ी है, हालांकि वे थोड़ा अलग लगते हैं:

1. पलक की लंबाई के नाय-डी क्वद-चूहे।

2. नाय-डी क्वद-चूहे पलक-रा की लंबाई का चूहा

मुझे ऐसा लगता है, क्या आपने आसानी से उनके साथ प्रबंधन किया है? चेक:

1. और यह चौकसता पर है) हम पहले से ही वैक्टर के निर्देशांक और पहले मिल चुके हैं :. फिर वेक्टर के निर्देशांक हैं। इसकी लंबाई का वर्ग बराबर होगा:

2. वेक्टर निर्देशांक खोजें

फिर इसकी लंबाई का वर्ग बराबर है

कुछ भी मुश्किल नहीं है, है ना? साधारण अंकगणित, और नहीं।

निम्नलिखित कार्यों को स्पष्ट रूप से वर्गीकृत नहीं किया जा सकता है, वे एक सामान्य विद्रोह की तरह हैं और क्षमता में सरल चित्रों को आकर्षित करने के लिए।

1. एनए-डी साइनस को कोने-केलो-ऑन-कट, सह-इकाई-इन-वाई-वें पॉइंट के कोने के कोण, एब्सिसा अक्ष के साथ।

तथा

हम यहाँ कैसे आएंगे? एक्सिस के बीच साइन कोण को ढूंढना आवश्यक है। और हम कहाँ जानते हैं कि साइनस की तलाश कैसे करें? एक आयताकार त्रिभुज में। तो हमें क्या करने की ज़रूरत है? इस त्रिकोण का निर्माण!

चूंकि बिंदु के निर्देशांक और, तब सेगमेंट बराबर है, और सेगमेंट। हमें एक साइन कोने खोजने की जरूरत है। मैं आपको याद दिलाऊंगा कि साइनस हाइपोटेन्यूज़ के लिए विपरीत कैटेक का रवैया है, फिर

हमें क्या करना है? Hypotenuse खोजें। आप इसे दो तरीकों से कर सकते हैं: पायथागोर प्रमेय (कैटनेट्स ज्ञात हैं!) या दो बिंदुओं के बीच दूरी सूत्र द्वारा (वास्तव में एक ही चीज़ के रूप में एक ही चीज़!)। मैं दूसरी बार जाऊंगा:

उत्तर:

अगला कार्य आपको भी आसान लगेगा। वह बिंदु के निर्देशांक पर है।

कार्य 2। एबीएस एक्सिस पर oposchn पेन-पेन-डी-झूठ के बिंदु से। नाई-डाइट एबीएस सीआईएस-एसयू ओएस-नो-वाया-पेन-डी-कु-ला-आरए।

चलो एक ड्राइंग बनाते हैं:

लंबवत का आधार वह बिंदु है जिसमें यह एब्सिसा अक्ष (एक्सिस) को पार करता है बिंदु है। चित्र दिखाता है कि इसके निर्देशांक हैं :. हम abscissa में रुचि रखते हैं - यानी, "औंस" घटक। यह बराबर है।

उत्तर: .

कार्य 3। पिछले कार्य की शर्तों के तहत, बिंदु से समन्वय अक्ष तक की दूरी की मात्रा पाएं।

कार्य आमतौर पर प्राथमिक होता है यदि आप जानते हैं कि अंक से अक्ष तक दूरी क्या है। आपको पता है? मुझे उम्मीद है, लेकिन अभी भी आपको याद दिलाता है:

तो, मेरे ड्राइंग पर, ऊपर स्थित, मैंने पहले से ही एक ऐसे लंबवत को चित्रित किया है? एक्सिस क्या है? धुरी के लिए। और उसकी लंबाई की लंबाई क्या है? यह बराबर है। अब मेरे पास धुरी के लिए एक लंबवत है और इसे लंबाई मिलती है। यह बराबर होगा, है ना? तब उनकी राशि बराबर है।

उत्तर: .

कार्य 4। समस्याओं के संदर्भ में, बिंदु के क्रम को ढूंढें, अवशोषित अक्ष के सापेक्ष सममित बिंदु।

मुझे लगता है कि आप सहज रूप से स्पष्ट हैं कि समरूपता क्या है? बहुत सारी ऑब्जेक्ट्स में है: कई इमारतों, टेबल, हवाई जहाज, कई ज्यामितीय आकार: गेंद, सिलेंडर, स्क्वायर, रम्बस इत्यादि। मोटे तौर पर बोलते हुए, समरूपता को समझा जा सकता है: इस आंकड़े में दो (या अधिक) समान हिस्सों होते हैं। इस तरह की समरूपता अक्षीय कहा जाता है। एक्सिस क्या है? यह वही पंक्ति है जिसमें आंकड़ा अपेक्षाकृत बोल रहा है, एक ही हिस्सों पर "कट" (इस तस्वीर में समरूपता की धुरी सीधे है):

अब चलो हमारे काम पर वापस जाएं। हम जानते हैं कि हम एक बिंदु की तलाश में हैं, धुरी के बारे में सममित। फिर यह धुरी समरूपता धुरी है। इसलिए हमें इस तरह के एक बिंदु का उल्लेख करने की आवश्यकता है ताकि अक्ष सेगमेंट को दो बराबर भागों में काट सके। इस तरह के एक बिंदु का जश्न मनाने के लिए खुद को आज़माएं। और अब मेरे निर्णय के साथ तुलना करें:

क्या तुमने ऐसा ही किया? ठीक है! पाया गया बिंदु पर हम साधारण में रुचि रखते हैं। यह बराबर है

उत्तर:

और अब मुझे बताएं, सेकंड सोचें, एब्सिसा पॉइंट क्या होगा, सममित बिंदु एक समन्वय धुरी के सापेक्ष क्या होगा? आपका जवाब क्या है? सही जवाब: ।

सामान्य मामले में, नियम इस तरह लिखा जा सकता है:

बिंदु, एब्सिसा अक्ष के सापेक्ष सममित बिंदु, निर्देशांक है:

बिंदु, समन्वय धुरी के सापेक्ष सममित बिंदु, निर्देशांक है:

खैर, अब काफी भयानक है एक कार्य: निर्देशांक की शुरुआत के सापेक्ष बिंदु, सममित बिंदु के निर्देशांक खोजें। सबसे पहले, अपने बारे में सोचें, और फिर मेरी ड्राइंग देखें!

उत्तर:

अब क पोलोग्राम समस्या:

कार्य 5: जावा-वे-सिया वेर-शि-ना पैराले-ले-लो ग्राम मा के अंक। नाय-डाई या-डी-ऑन-पॉइंट।

आप इस समस्या को दो तरीकों से हल कर सकते हैं: समन्वय की तर्क और विधि। मैं पहले समन्वय विधि लागू करता हूं, और फिर मैं आपको बताऊंगा कि अन्यथा कैसे हल किया जाए।

यह स्पष्ट है कि Abscissa बिंदु बराबर है। (यह बिंदु से Abscissa अक्ष तक आयोजित एक लंबवत पर स्थित है)। हमें ordinate खोजने की जरूरत है। हम इस तथ्य का उपयोग करते हैं कि हमारा आंकड़ा एक समानांतर है, इसका मतलब है कि। दो बिंदुओं के बीच दूरी सूत्र का उपयोग करके सेगमेंट की लंबाई पाएं:

धुरी के साथ बिंदु को जोड़ने वाले लंबवत को कम करें। चौराहा बिंदु पत्र इंगित करेगा।

सेगमेंट की लंबाई बराबर है। (कार्य को स्वयं ढूंढें, जहां हमने इस पल पर चर्चा की), तो हमें पाइथागोरा प्रमेय पर सेगमेंट की लंबाई मिलती है:

सेगमेंट की लंबाई - बिल्कुल इसके समन्वय के साथ मेल खाता है।

उत्तर: .

एक और समाधान (मैं सिर्फ एक तस्वीर दे दूंगा जो इसे दिखाता है)

समाधान:

1. आचरण

2. बिंदु और लंबाई के निर्देशांक का पता लगाएं

3. साबित करो।

एक और कटौती की समस्या:

जावा-ल्यूब-सिया वेर-शि-ऑन-एमआई ट्रे-कोयला-नी के अंक। Nai di अपनी मध्यम रेखा की लंबाई, पैराले-लेले।

क्या आपको याद है कि त्रिभुज की मध्य रेखा क्या है? फिर आपके लिए यह कार्य प्राथमिक है। अगर आपको याद नहीं है, तो मैं आपको याद दिलाऊंगा: त्रिभुज की मध्य रेखा एक ऐसी रेखा है जो मध्य-विपरीत पक्षों को जोड़ती है। यह आधार के समानांतर है और आधे आधे के बराबर है।

आधार एक सेगमेंट है। इसकी लंबाई हमें पहले देखना पड़ा, यह बराबर है। फिर मध्य रेखा की लंबाई आधा छोटा और बराबर है।

उत्तर: .

टिप्पणी: इस कार्य को एक और तरीके से हल किया जा सकता है जिसके लिए हम थोड़ी देर बाद बदलते हैं।

इस बीच, अब आपके पास कुछ कार्य हैं, उन पर ले जाएं, वे पूरी तरह से सरल हैं, लेकिन समन्वय विधि के उपयोग पर "हाथ भरें" में मदद करें!

1. जावा-ला-सिया वेर-शि-ऑन-टूर-पैन के अंक। एनएआई डीएस अपने पर्यावरण लाइन की लंबाई।

2. अंक और जावा-डब्ल्यूए-सिया वे-शि-ना पैराले-ले-लो ग्राम मा। नाय-डाई या-डी-ऑन-पॉइंट।

3. कट-का, सह-इकाई-एनवाई-वाई-वें बिंदु से नाय-डी लंबाई और

4. सह-या-एनयू फ्लैट-सह-पीओ पर क्राई-शान-जैसे एफ-गु-आरवाई के नाई डी-ट्यूर्स।

5. बिंदु के माध्यम से ऑन-चा-ले सह-या-डी-एनएटी प्रो-हो-डिट में एक मूल्य-ट्रूम के आसपास। नहीं-di उसकी Ra di-Musty।

6. नाय-डि-डी-डी-शि-नो-पोसी, ओपीआई-सान-नो रॉड-मो-कंप्यूट-एनआई-का, वेर-शि-आरओ -डीआई-ऑन-आप सह-से-पशु चिकित्सक

समाधान:

1. यह ज्ञात है कि ट्रेपेज़ियम की मध्य रेखा आधार के बराबर है। आधार बराबर है, और आधार। फिर

उत्तर:

2. इस कार्य को हल करने का सबसे आसान तरीका है: ध्यान दें कि (समांतरोग्राम का नियम)। वैक्टर के निर्देशांक की गणना करें और संभव नहीं है :. इसके अलावा, समन्वय वैक्टरों को तब्दील कर दिया जाता है। फिर निर्देशांक है। वही निर्देशांक भी एक बिंदु है, क्योंकि वेक्टर की शुरुआत निर्देशांक के साथ एक बिंदु है। हम साधारण में रुचि रखते हैं। यह बराबर है।

उत्तर:

3. हम दो बिंदुओं के बीच दूरी सूत्र से तुरंत कार्य करते हैं:

उत्तर:

4. तस्वीर को देखो और कहें, जिसके बीच दो आंकड़े छायांकित क्षेत्र "क्लैंप" हैं? यह दो वर्गों के बीच क्लैंप किया गया है। फिर वांछित आंकड़ा का क्षेत्र एक बड़े वर्ग शून्य के वर्ग के बराबर है वर्ग छोटा है। एक छोटे वर्ग का पक्ष एक सेगमेंट कनेक्टिंग पॉइंट्स है और इसकी लंबाई बराबर है

तब छोटा वर्ग वर्ग बराबर है

इसी प्रकार, एक बड़े वर्ग के साथ: उसका पक्ष एक सेगमेंट कनेक्टिंग पॉइंट्स है और इसकी लंबाई बराबर है

तब बड़ा वर्ग वर्ग बराबर है

इच्छित आंकड़ा सूत्र द्वारा पाएंगे:

उत्तर:

5. यदि सर्कल में एक केंद्र के रूप में मूल होता है और बिंदु के माध्यम से गुजरता है, तो इसका त्रिज्या वास्तव में सेगमेंट की लंबाई के बराबर होगा (एक ड्राइंग बनाएं और आप समझेंगे कि यह स्पष्ट क्यों है)। इस सेगमेंट की लंबाई पाएं:

उत्तर:

6. यह ज्ञात है कि आयताकार के पास वर्णित परिधि का त्रिज्या इसके विकर्ण के आधे के बराबर है। हम किसी भी दो विकर्णों की लंबाई पाएंगे (आखिरकार, एक आयताकार में वे बराबर हैं!)

उत्तर:

खैर, आपने सब कुछ के साथ मुकाबला किया? यह पता लगाना बहुत मुश्किल नहीं था, क्योंकि ऐसा है? यहां नियम एक बात है - एक दृश्य चित्र बनाने में सक्षम होने के लिए और बस सभी डेटा से "गिनती" करें।

हमने काफी कुछ छोड़ दिया। अभी भी सचमुच दो अंक हैं जिन्हें मैं चर्चा करना चाहूंगा।

आइए यह तय करने की कोशिश करें कि यह एक साधारण काम है। दो अंक और। सेगमेंट के बीच के निर्देशांक का पता लगाएं। इस कार्य का समाधान निम्न है: बिंदु को दें - मध्य की खोज, फिर निर्देशांक:

अर्थात: सेगमेंट के बीच के निर्देशांक \u003d सेगमेंट के अंत के समन्वय के अंकगणितीय औसत।

यह नियम बहुत आसान है और एक नियम के रूप में छात्रों में कठिनाइयों का कारण नहीं बनता है। आइए देखें कि कौन से कार्य और इसका उपयोग कैसे किया जाता है:

1. नाय-डी या-डी-ऑन-टीयू एसई-डी-डी-कट, सह-इकाई-एनवाई-यू-वें बिंदु और

2. जावा-ल्यूब-सिया वेर-शि-ना-एमआई-ट्वह-कोयला-नी-का अंक। अपने डी-गो-ऑन-लेई के नाय-डी या-डी-ऑन-टीए डॉट्स।

3. नाई-डि एबीएस-एसयू-एसयू प्राइस-ट्रा आसपास पड़ोस के आसपास, ओपीआई-सान-सान दाईं ओर-एनआई-का, वेर-शि-आरओ सह-या-डी-ऑन-यू सह ओटी-पशु चिकित्सक।

समाधान:

1. पहला कार्य सिर्फ एक क्लासिक है। हम सेगमेंट के बीच की परिभाषा के तुरंत बाद कार्य करते हैं। इसके निर्देशांक हैं। Ordinate बराबर है।

उत्तर:

2. यह देखना आसान है कि यह चतुर्भुज एक समांतरोग्राम (यहां तक \u200b\u200bकि rhombus!) है। आप स्वयं इसे स्वयं साबित कर सकते हैं, पार्टियों की लंबाई की गणना और स्वयं के बीच उनकी तुलना कर सकते हैं। समांतरोग्राम के बारे में मुझे क्या पता है? चौराहे का उनका विकर्ण बिंदु आधे में बांटा गया है! हाँ! तो विकर्णों के चौराहे का बिंदु क्या है? यह किसी भी विकर्ण का एक मध्य है! विशेष रूप से, विकर्ण का चयन करें। फिर बिंदु में समन्वय बिंदु के समन्वय होते हैं।

उत्तर:

3. सर्कल आयताकार के पास वर्णित केंद्र का संयोग क्या है? यह उनके विकर्ण के चौराहे बिंदु के साथ मेल खाता है। और आप आयत के विकर्ण के बारे में क्या जानते हैं? वे बराबर हैं और चौराहे बिंदु आधे से विभाजित है। कार्य पिछले एक के लिए चला गया था। मैं ले जाऊंगा, उदाहरण के लिए, विकर्ण। फिर यदि वर्णित सर्कल का केंद्र, फिर मध्य। निर्देशांक की तलाश में: अनुपस्थिति बराबर है।

उत्तर:

अब थोड़ा अकेला अभ्यास करें, मैं केवल प्रत्येक कार्य के जवाब दूंगा ताकि आप स्वयं को जांच सकें।

1. नाय-डी-टी-डी-शि-नो-ई, ओपीआई-सान ट्रे-कोयला-नी-का, वे-शि-गो-आरओ के बारे में सह-शि-गो-आरओ सह-या-डि-नहीं है

2. नाय-डी-टी-डी-ओ-तु-टूर डिस्कीबेम्बर-नो, ओपीआई-सान-नो प्रोटेज-नी-का, वेर-शि-गो-रो समन्वय करता है

3. का-को-गो-डी-यू-एसए को एक मूल्य-ट्रिपल से घिरा हुआ होना चाहिए ताकि वह एसए-लास एक्सिस एबीएस कर सके?

4. एनए-डी या-डी-ऑन-टीए एक्सिस की धुरी के धुरी और कटौती, सह-इकाई-यू-वें बिंदु और

उत्तर:

सब कुछ सफल हुआ? मैं वास्तव में इसके लिए आशा करता हूँ! अब - अंतिम झटका। अब विशेष रूप से चौकस हो। वह सामग्री जो अब मैं समझाऊंगा अब सीधे भाग के समन्वय विधि पर सरल कार्यों के लिए सीधे संबंधित है, बल्कि कार्य सी 2 में भी हर जगह होती है।

मेरे कौन से वादे मैंने अभी तक संयमित नहीं किया है? याद रखें कि वैक्टरों पर मैंने किन संचालन को प्रवेश करने का वादा किया और आखिरकार क्या पेश किया? मैं बिल्कुल नहीं भूल गया? भूल गया! मैं यह बताना भूल गया कि वैक्टर का गुणा क्या है।

वेक्टर पर वेक्टर को गुणा करने के दो तरीके हैं। चयनित विधि के आधार पर, हमारे पास विभिन्न प्रकृति की वस्तुएं होंगी:

वेक्टर उत्पाद सुंदर चालाक किया जाता है। इसे कैसे करें और यह आवश्यक क्यों है, हम अगले लेख में चर्चा करेंगे। और इसमें हम स्केलर उत्पाद पर ध्यान केंद्रित करेंगे।

हमें गणना करने की अनुमति देने के लिए पहले से ही दो तरीके हैं:

जैसा कि आपने अनुमान लगाया है, परिणाम वही होना चाहिए! तो, आइए पहले पहले तरीके से विचार करें:

समन्वय के माध्यम से स्केलर उत्पाद

खोजें: - एक स्केलर उत्पाद का आम तौर पर स्वीकृत संकेत

गणना के लिए फॉर्मूला अगला:

यही है, स्केलर उत्पाद \u003d वैक्टर के निर्देशांक के कार्यों की मात्रा!

उदाहरण:

नाई डि

फेसला:

हम प्रत्येक वैक्टर के निर्देशांक पाएंगे:

सूत्र द्वारा स्केलर उत्पाद की गणना करें:

उत्तर:

देखो, बिल्कुल कुछ जटिल नहीं!

खैर, अब खुद को आजमाएं:

· घटनाओं की नाय-डी स्का-लार-नी प्रो-वी-डी-डी-

सामना? शायद मैंने छल को छोटा देखा? चलो देखते है:

पिछले कार्य में वैक्टर के निर्देशांक! उत्तर :.

समन्वय के अलावा, स्केलर उत्पाद की गणना करने का एक और तरीका है, अर्थात्, उनके बीच वैक्टर और कोसाइन कोण की लंबाई के माध्यम से:

वैक्टर के बीच कोण को इंगित करता है और।

यही है, स्केलर उत्पाद उनके बीच कोने के कोने की कोसाइन पर वैक्टर की लंबाई के उत्पाद के बराबर है।

हमारे पास यह दूसरा सूत्र क्यों है यदि हमारे पास पहला है जो बहुत आसान है, इसमें कम से कम कोई कोसाइन नहीं है। और इस तथ्य के लिए जरूरी है कि पहले और दूसरे सूत्र से हम वैक्टर के बीच कोण को कैसे ढूंढ सकते हैं!

फिर वेक्टर की लंबाई के लिए सूत्र याद रखें!

फिर अगर मैं इस डेटा को स्केलर उत्पाद के सूत्र में प्रतिस्थापित करता हूं, तो मुझे मिलेगा:

लेकिन दूसरी तरफ:

तो मुझे तुम्हारे पास क्या मिला? अब हमारे पास एक सूत्र है जो आपको दो वैक्टरों के बीच कोण की गणना करने की अनुमति देता है! कभी-कभी यह संक्षिप्तता के लिए भी लिखा जाता है:

यही है, वैक्टर के बीच कोण की गणना के लिए एल्गोरिदम निम्नानुसार है:

1. निर्देशांक के माध्यम से स्केलर उत्पाद की गणना करें
2. हम वैक्टर की लंबाई पाते हैं और उन्हें बाहर कर देते हैं
3. हम क्लॉज 2 के परिणाम पर खंड 1 के परिणाम को विभाजित करते हैं

आइए उदाहरणों में अभ्यास करें:

1. आंखों को पलक-रे के बीच कोने और। Gra-du-Sac में जवाब दें।

2. पिछले कार्य की शर्तों के तहत, वैक्टर के बीच कोसाइन खोजें।

हम यह करेंगे: पहला कार्य मैं आपको तय करने में मदद करूंगा, और दूसरा स्वयं करने की कोशिश करूंगा! मैं सहमत हूं? फिर शुरू करो!

1. ये वेक्टर हमारे पुराने परिचित हैं। हमने पहले ही अपने स्केलर का काम माना और यह बराबर था। उनके पास ऐसे निर्देशांक हैं :, फिर हमें उनकी लंबाई मिलती है:

फिर हम वैक्टर के बीच एक कोसाइन की तलाश में हैं:

कोसिनस कौन सा कोने बराबर है? यह कोण है।

उत्तर:

खैर, अब मैं खुद दूसरे कार्य को हल करता हूं, और फिर तुलना करता हूं! मैं केवल एक बहुत ही संक्षिप्त समाधान दूंगा:

2. इसके निर्देशांक हैं, निर्देशांक हैं।

चलो - वैक्टर के बीच कोण और फिर

उत्तर:

यह ध्यान दिया जाना चाहिए कि कार्य सीधे वेक्टर में हैं और परीक्षा कार्य के भाग बी में समन्वय विधि दुर्लभ है। हालांकि, समन्वय प्रणाली के परिचय का सहारा लेकर सी 2 कार्यों के भारी बहुमत को आसानी से हल किया जा सकता है। तो आप इस आलेख को नींव से मान सकते हैं, जिसके आधार पर हम पर्याप्त मुश्किल निर्माण करेंगे, जो जटिल कार्यों को हल करने के लिए आवश्यक होंगे।

निर्देशांक और वैक्टर। मध्य-रोविंग

हम समन्वय विधि का अध्ययन जारी रखते हैं। अंतिम भाग में, हमने कई महत्वपूर्ण सूत्र लाए जो अनुमति देते हैं:

1. वेक्टर के निर्देशांक का पता लगाएं
2. वेक्टर की लंबाई (वैकल्पिक: दो बिंदुओं के बीच की दूरी)
3. फोल्ड, वेक्टर घटाएं। उन्हें वास्तविक संख्या में गुणा करें
4. एक मध्य कटौती का पता लगाएं
5. वैक्टर के स्केलर उत्पाद की गणना करें
6. वैक्टर के बीच कोण खोजें

बेशक, संपूर्ण समन्वय विधि इन 6 अंकों में फिट नहीं होती है। यह एक विश्लेषणात्मक ज्यामिति के रूप में इस तरह के विज्ञान को रेखांकित करता है जिसके साथ आपको विश्वविद्यालय को जानना है। मैं सिर्फ एक नींव बनाना चाहता हूं जो आपको एक ही राज्य में समस्याओं को हल करने की अनुमति देगा। परीक्षा। भाग बी के कार्यों के साथ हमने पाया कि अब गुणात्मक रूप से नए स्तर पर जाने का समय है! यह आलेख उन सी 2 कार्यों को हल करने की विधि को समर्पित किया जाएगा, जिसमें समन्वय विधि में जाने के लिए यह उचित होगा। यह तर्कसंगतता इस तथ्य से निर्धारित की जाती है कि कार्य को खोजने के लिए आवश्यक है और कौन सा आंकड़ा दिया गया है। इसलिए, यदि आप जारी किए जाते हैं तो मैं समन्वय विधि लागू करूंगा:

1. दो विमानों के बीच कोण का पता लगाएं
2. सीधे और विमान के बीच कोण का पता लगाएं
3. दो सीधे के बीच कोण का पता लगाएं
4. बिंदु से विमान तक की दूरी का पता लगाएं
5. बिंदु से सीधे दूरी का पता लगाएं
6. लाइन से विमान की दूरी का पता लगाएं
7. दो सीधे के बीच की दूरी का पता लगाएं

यदि समस्या की स्थिति में आकृति रोटेशन का शरीर है (गेंद, सिलेंडर, शंकु ...)

समन्वय विधि के लिए उपयुक्त आंकड़े हैं:

1. आयताकार समानांतर
2. पिरामिड (त्रिकोणीय, चतुर्भुज, हेक्सागोनल)

मेरे अनुभव में भी इसके लिए समन्वय विधि का उपयोग करने के लिए अव्यवहारिक है:

1. वर्गों के क्षेत्रों की तलाश में
2. वॉल्यूम्स की गणना

हालांकि, यह तुरंत ध्यान दिया जाना चाहिए कि अभ्यास में समन्वय स्थिति की विधि के लिए तीन "लाभहीन" काफी दुर्लभ है। अधिकांश कार्यों में, वह आपके उद्धारकर्ता बन सकता है, खासकर यदि आप त्रि-आयामी इमारतों में बहुत मजबूत नहीं हैं (जो कभी-कभी काफी जटिल होते हैं)।

उपरोक्त सभी आंकड़े क्या हैं? वे अब फ्लैट नहीं हैं, उदाहरण के लिए, एक वर्ग, त्रिकोण, सर्कल, और थोक! तदनुसार, हमें दो-आयामी, लेकिन त्रि-आयामी समन्वय प्रणाली पर विचार करने की आवश्यकता नहीं है। यह काफी आसान है: एब्सिसा और अध्यादेशों की धुरी के अलावा, हम एक और धुरी, एप्लाइड एक्सिस पेश करते हैं। यह आंकड़ा योजनाबद्ध रूप से उनके पारस्परिक स्थान दिखाता है:

वे सभी पारस्परिक रूप से लंबवत हैं, एक बिंदु पर छेड़छाड़ करते हैं, जिसे हम निर्देशांक की शुरुआत को बुलाएंगे। पहले के रूप में, Abscissa की धुरी, हम ordinate की धुरी को दर्शाते हैं - और आवेदन की पेश की गई धुरी -।

यदि पहले विमान पर प्रत्येक बिंदु को दो संख्याओं द्वारा विशेषता दी गई थी - ABSCISSA और सामान्य, तो अंतरिक्ष में प्रत्येक बिंदु पहले से ही तीन संख्याओं - Abscissa, ordinate, applikate द्वारा वर्णित है। उदाहरण के लिए:

तदनुसार, बिंदु का एब्सिसा बराबर, ordinate -, और आवेदक है -।

कभी-कभी एब्सिसा पॉइंट को एब्रिसा अक्ष पर बिंदु का प्रक्षेपण भी कहा जाता है, ऑर्डिनेट - ऑर्डिनेट की धुरी पर बिंदु का प्रक्षेपण, और आवेदन - एप्लिकेट अक्ष पर बिंदु का प्रक्षेपण। तदनुसार, यदि बिंदु सेट है, तो निर्देशांक के साथ बिंदु:

विमान को प्रक्षेपण बिंदु पर कॉल करें

विमान को प्रक्षेपण बिंदु पर कॉल करें

प्राकृतिक प्रश्न उठता है: क्या अंतरिक्ष में द्वि-आयामी मामले के लिए सभी सूत्र व्युत्पन्न हैं? जवाब सकारात्मक है, वे निष्पक्ष हैं और समान रूप से समान हैं। एक छोटी सी जानकारी के लिए। मुझे लगता है कि आपने पहले ही अपने आप को अनुमान लगाया है। सभी सूत्रों में, हमें एप्लिकेट अक्ष के लिए जिम्मेदार एक और सदस्य जोड़ना होगा। अर्थात्।

1. यदि दो बिंदु सेट हैं: तो:

• वेक्टर के निर्देशांक:
• दो बिंदुओं (या वेक्टर की लंबाई) के बीच की दूरी
• सेगमेंट के बीच में निर्देशांक हैं

2. यदि दो संस्करण दिए गए हैं: और फिर:

• उनका स्केलर उत्पाद है:
• वैक्टर के बीच कोसाइन कोण है:

हालांकि, अंतरिक्ष इतना आसान नहीं है। जैसा कि आप समझते हैं, एक और समन्वय जोड़ना इस अंतरिक्ष में आंकड़ों के स्पेक्ट्रम में एक महत्वपूर्ण विविधता बनाता है, "जीवित"। और आगे की नरेशन के लिए, मुझे कुछ, मोटे तौर पर बोलते हुए, "सामान्यीकरण" को शुरू करने की आवश्यकता है। यह "सामान्यीकरण" विमान होगा। आप विमान के बारे में क्या जानते हैं? प्रश्न का उत्तर देने की कोशिश करें, और एक विमान क्या है? यह कहना बहुत मुश्किल है। हालांकि, हम सभी सहजता से कल्पना करते हैं कि यह कैसा दिखता है:

लगभग बोलते हुए, यह एक गैर-अनंत "पत्ती" है, जो अंतरिक्ष में शामिल है। "इन्फिनिटी" को समझा जाना चाहिए कि विमान सभी दिशाओं पर लागू होता है, यानी, इसका क्षेत्र अनंत के बराबर है। हालांकि, यह स्पष्टीकरण "उंगलियों पर" विमान की संरचना का मामूली विचार नहीं देता है। और इसमें दिलचस्पी होगी।

आइए ज्यामिति की मुख्य अक्षों में से एक को याद रखें:

• विमान पर दो अलग-अलग बिंदुओं के माध्यम से, यह सीधे एक के साथ जाता है:

या अंतरिक्ष में इसकी एनालॉग:

बेशक, आपको याद है कि समीकरण को सीधे दो पूर्व निर्धारित बिंदुओं में कैसे हटाया जाए: यदि पहले बिंदु के निर्देशांक: और दूसरा, तो प्रत्यक्ष समीकरण निम्नानुसार होगा:

आप 7 वीं कक्षा में पारित हुए। अंतरिक्ष में, प्रत्यक्ष समीकरण इस तरह दिखता है: आइए निर्देशांक के साथ दो अंक दें:, समीकरण सीधे गुजरने के माध्यम से, उपस्थिति है:

उदाहरण के लिए, अंक के माध्यम से, सीधी रेखा गुजरती है:

इसे कैसे समझा जाना चाहिए? यह समझा जाना चाहिए: बिंदु उस पंक्ति पर स्थित है यदि इसके निर्देशांक निम्नलिखित सिस्टम को संतुष्ट करते हैं:

हम वास्तव में समीकरण में सीधे रुचि नहीं लेंगे, लेकिन हमें सीधे वैक्टर की बहुत ही महत्वपूर्ण अवधारणा पर ध्यान देना होगा। - कोई भी नॉनज़रो वेक्टर इस प्रत्यक्ष या समानांतर पर झूठ बोल रहा है।

उदाहरण के लिए, दोनों वैक्टर निर्देशक निर्देशक हैं। बिंदु पर झूठ बोलने दो, और इसके मार्गदर्शक वेक्टर। फिर समीकरण प्रत्यक्ष निम्नलिखित रूप में लिखा जा सकता है:

मैं एक बार फिर दोहराता हूं, मैं सीधे समीकरण में रूचि नहीं रखूंगा, लेकिन मुझे वास्तव में आपको याद रखने की आवश्यकता है कि गाइड वेक्टर क्या है! फिर व: यह किसी भी बकवास वेक्टर एक सीधी रेखा पर स्थित है, या इसके समानांतर है।

प्रदर्शन तीन निर्दिष्ट बिंदुओं के लिए विमान का समीकरण इतना तुच्छ नहीं है, और आमतौर पर इस सवाल को हाई स्कूल से अवगत नहीं माना जाता है। और व्यर्थ में! जब हम जटिल कार्यों को हल करने के लिए समन्वय विधि का सहारा लेते हैं तो यह तकनीक महत्वपूर्ण होती है। हालांकि, मुझे लगता है कि आप कुछ नया सीखने की इच्छा से भरे हुए हैं? इसके अलावा, आप विश्वविद्यालय में अपने शिक्षक को हिट कर सकते हैं जब यह पता चला है कि आप पहले से ही जानते हैं कि आप पहले से ही एक तकनीक के साथ कैसे हैं जो आमतौर पर विश्लेषणात्मक ज्यामिति के दौरान अध्ययन किया जाता है। तो, आगे बढ़ें।

विमान समीकरण विमान पर प्रत्यक्ष समीकरण से बहुत अलग नहीं है, अर्थात् यह दिखता है:

कुछ संख्याएं (सभी बराबर शून्य नहीं), और चर, उदाहरण के लिए: आदि जैसा कि आप देख सकते हैं, विमान का समीकरण सीधी रेखा (रैखिक फ़ंक्शन) के समीकरण से बहुत अलग नहीं है। हालांकि, याद रखें कि हमने आपके साथ तर्क दिया है? हमने कहा कि यदि हमारे पास तीन अंक हैं जो एक सीधी रेखा पर झूठ नहीं बोल रहे हैं, तो विमान के समीकरण निश्चित रूप से उनके द्वारा बहाल किए गए हैं। पर कैसे? मैं आपको समझाने की कोशिश करूंगा।

चूंकि विमान समीकरण है:

और अंक इस विमान से संबंधित हैं, फिर विमान समीकरण के प्रत्येक बिंदु के निर्देशांक को प्रतिस्थापित करते समय, हमें एक वास्तविक पहचान प्राप्त करनी चाहिए:

इस प्रकार, यह पहले से ही अज्ञात के साथ तीन समीकरणों को हल करने के लिए आवश्यक हो जाता है! दुविधा! हालांकि, यह हमेशा माना जा सकता है कि (इसके लिए आपको विभाजित करने की आवश्यकता है)। इस प्रकार, हम तीन अज्ञात के साथ तीन समीकरण प्राप्त करते हैं:

हालांकि, हम ऐसी प्रणाली को हल नहीं करेंगे, और हम उस रहस्यमय अभिव्यक्ति को बदल देंगे जो इससे इस प्रकार है:

तीन सेटपॉइंट्स के माध्यम से गुजरने वाले विमान का समीकरण

\\ [\\ Left | (\\ _ प्रारंभ (20) (c)) (x - (x_0)) & ((x_1) - (x_0)) & ((x_2) - (x_0) - (x_0)) \\\\ (y - (y_0) ) और ((y_1) - (y_0)) & ((y_2) - (y_0)) \\\\ (z - (z_0)) & ((Z_1) - (Z_0)) & ((Z_2) - (Z_0)) \\ End (सरणी)) \\ अधिकार | \u003d 0 \\]

रुकें! और क्या है? कुछ बहुत ही असामान्य मॉड्यूल! हालांकि, जिस वस्तु को आप अपने सामने देखते हैं, उसके पास मॉड्यूल से कोई लेना-देना नहीं है। इस वस्तु को तीसरा आदेश निर्धारक कहा जाता है। अब से, भविष्य में, जब आप विमान पर समन्वय विधि से निपट रहे हैं, तो आप अक्सर इन पहचानों को पूरा करेंगे। तीसरा आदेश निर्धारक क्या है? विचित्र रूप से पर्याप्त, यह सिर्फ एक संख्या है। यह समझने के लिए बनी हुई है कि विशेष रूप से संख्या जो हम निर्धारक के साथ तुलना करेंगे।

आइए पहले एक सामान्य रूप में तीसरे क्रम निर्धारक लिखें:

कुछ संख्याएँ कहां हैं। और पहली सूचकांक के तहत, हम लाइन संख्या को समझते हैं, और सूचकांक के तहत - कॉलम की संख्या। उदाहरण के लिए, इसका मतलब है कि यह संख्या दूसरी पंक्ति और तीसरे कॉलम के चौराहे पर है। आइए निम्नलिखित प्रश्न उठाएं: हम इस तरह के एक निर्धारक की गणना कैसे करेंगे? यही है, हम किस विशिष्ट संख्या की तुलना करेंगे? एक तीसरे क्रम के निर्धारक के लिए, एक ह्यूरिस्टिक (दृश्य) त्रिकोण नियम है जो ऐसा लगता है:

1. मुख्य विकर्ण (ऊपरी बाएं कोने से निचले दाएं तक) के तत्वों का उत्पाद पहला त्रिभुज "लंबवत" मुख्य विकर्ण बनाने वाले तत्वों का उत्पाद दूसरे त्रिभुज "लंबवत" मुख्य विकर्ण बनाने वाले तत्वों का उत्पाद बनाता है
2. साइड विकर्ण (निचले दाएं कोण से निचले बाएं से) के तत्वों का उत्पाद दूसरे त्रिकोण द्वारा पहला त्रिकोण "लंबवत" बनाने वाले तत्वों का उत्पाद दूसरा त्रिभुज "लंबवत" पक्ष विकर्ण बनाने वाले तत्वों के उत्पाद का उत्पाद
3. फिर निर्धारक कदम में प्राप्त मूल्यों के अंतर के बराबर है और

यदि आप इन सभी संख्याओं को लिखते हैं, तो हमें निम्नलिखित अभिव्यक्ति मिल जाएगी:

फिर भी, इस फॉर्म में गणना की विधि को याद रखना जरूरी नहीं है, यह केवल त्रिकोण और विचार को रखने के लिए सिर में पर्याप्त है, जो कि यह बनाता है और फिर कुछ से कटौती की जाती है)।

आइए उदाहरण पर त्रिभुज विधि को चित्रित करें:

1. निर्धारक की गणना करें:

आइए हम जो गुना करते हैं उससे निपटते हैं, और क्या - हम घटाते हैं:

"प्लस" के साथ जाने वाले घटक:

यह मुख्य विकर्ण है: तत्वों का उत्पाद बराबर है

पहला त्रिकोण, "लंबवत मुख्य विकर्ण: तत्वों का उत्पाद बराबर है

दूसरा त्रिकोण, "लंबवत मुख्य विकर्ण: तत्वों का उत्पाद बराबर है

हम तीन संख्याओं को फोल्ड करते हैं:

"माइनस" के साथ जाने वाले घटक

यह एक पक्ष विकर्ण है: तत्वों का उत्पाद बराबर है

पहला त्रिभुज, "पक्ष विकर्ण के लंबवत: तत्वों का उत्पाद बराबर है

दूसरा त्रिकोण, "पक्ष विकर्ण के लिए लंबवत: तत्वों का उत्पाद बराबर है

हम तीन संख्याओं को फोल्ड करते हैं:

जो कुछ भी करना है वह "एक प्लस के साथ" शर्तों की राशि "के साथ" एक शून्य के साथ "शर्तों की राशि से कटौती करना है:

इस तरह,

जैसा कि आप देख सकते हैं, तीसरे क्रम के निर्धारकों की गणना में कुछ जटिल और अलौकिक नहीं है। त्रिकोणों के बारे में याद रखना और अंकगणितीय त्रुटियों की अनुमति नहीं देना महत्वपूर्ण है। अब खुद की गणना करने का प्रयास करें:

चेक:

1. पहला त्रिभुज, लंबवत मुख्य विकर्ण:
2. दूसरा त्रिकोण, लंबवत मुख्य विकर्ण:
3. प्लस के साथ शर्तों की राशि:
4. पक्ष विकर्ण के लिए लंबवत पहला त्रिभुज:
5. दूसरा त्रिभुज, पक्ष विकर्ण के लिए लंबवत:
6. एक ऋण के साथ शर्तों की राशि:
7. एक प्लस के साथ घटकों की मात्रा एक ऋण के साथ शर्तों की राशि से कम:

यहां एक और कुछ निर्धारक हैं, उन्होंने अपने अर्थों की गणना की और उत्तर के साथ तुलना की:

उत्तर:

खैर, सभी संयोग? बढ़िया, तो आप आगे बढ़ सकते हैं! यदि कठिनाइयों हैं, तो परिषद मेरा है: निर्धारक ऑनलाइन की गणना के लिए सॉफ्टवेयर का एक गुच्छा है। आपको बस अपनी पहचानकर्ता के साथ आने की ज़रूरत है, इसे स्वयं की गणना करें, और उसके बाद प्रोग्राम पर विचार करने के साथ तुलना करें। और तब तक जब परिणाम संयोग शुरू नहीं करते हैं। मुझे यकीन है कि यह पल इंतजार करने के लिए लंबे समय तक इंतजार नहीं करेगा!

अब चलिए निर्धारक पर वापस जाएं, जिसने लिखा था कि जब उन्होंने तीन सेटपॉइंट्स के माध्यम से विमान के समीकरण के समीकरण के बारे में बात की थी:

आपको केवल अपने मूल्य की गणना करना है (त्रिकोणों की विधि से) और परिणाम को शून्य तक बराबर करना। स्वाभाविक रूप से, क्योंकि - चर, फिर आपको उनके आधार पर कुछ अभिव्यक्ति मिल जाएगी। यह अभिव्यक्ति है जो तीन सेट बिंदुओं के माध्यम से गुजरने वाले विमान का समीकरण होगा जो एक सीधी रेखा पर झूठ नहीं बोल रहे हैं!

आइए उपरोक्त उदाहरण का वर्णन करें:

1. अंक के माध्यम से गुजरने वाले विमान के समीकरण का निर्माण

हम इन तीन बिंदुओं के लिए निर्धारक लिखते हैं:

सरल:

अब हम इसे त्रिकोण के नियम के अनुसार सीधे गणना करते हैं:

\\ [(\\ Left | (\\ BEGIN (सरणी) (* (20) (c)) (x + 3) और 2 & 6 \\\\ (y - 2) & 0 & 1 \\ (z + 1) & 5 & 0 \\ end (सरणी)) \\ राइट | \u003d \\ बाएं ((x + 3) \\ दाएं) \\ cdot 0 \\ cdot 0 + 2 \\ cdot 1 \\ cdot \\ बाएं ((जेड + 1) \\ राइट) + \\ Left ( (वाई - 2) \\ दाएं) \\ सीडीओटी 5 \\ सीडीओटी 6 -) \\]

इस प्रकार, अंक के माध्यम से गुजरने वाले विमान के समीकरण में फॉर्म है:

अब अपने आप को एक कार्य को हल करने का प्रयास करें, और फिर हम इस पर चर्चा करेंगे:

2. अंक के माध्यम से गुजरने वाले विमान के समीकरण का पता लगाएं

खैर, चलो अब निर्णय पर चर्चा करें:

हम एक निर्धारक बनाते हैं:

और इसके मूल्य की गणना करें:

फिर विमान का समीकरण है:

या, शॉर्टिंग, हमें मिलता है:

अब आत्म-नियंत्रण के लिए दो कार्य:

1. तीन बिंदुओं के माध्यम से गुजरने वाले विमान के समीकरण का निर्माण:

उत्तर:

सभी मेल खाते हैं? फिर, यदि कुछ कठिनाइयां हैं, तो मेरी सलाह है: आप मेरे सिर से तीन अंक लेते हैं (संभावना की एक बड़ी डिग्री के साथ वे एक सीधे पर झूठ नहीं बोलेंगे), उन पर एक विमान बनाएं। और फिर खुद को ऑनलाइन जांचें। उदाहरण के लिए, साइट पर:

हालांकि, निर्धारकों की मदद से, हम न केवल विमान के समीकरण का निर्माण करेंगे। याद रखें, मैंने आपको बताया कि वैक्टर न केवल स्केलर उत्पाद को परिभाषित करते हैं। अभी भी एक वेक्टर है, साथ ही मिश्रित काम भी है। और यदि दो वैक्टरों का स्केलर उत्पाद और वहां एक संख्या होगी, तो दो वैक्टरों के वेक्टर उत्पाद और वेक्टर होंगे, और यह वेक्टर निर्दिष्ट के लिए लंबवत होगा:

इसके अलावा, इसका मॉड्यूल समांतरोग्राम के क्षेत्र के बराबर होगा, जो वैक्टर से पहले और है। इस वेक्टर को बिंदु से दूरी की गणना करने की आवश्यकता होगी। हम वेक्टर के वेक्टर उत्पाद को कैसे मानते हैं और यदि उनके निर्देशांक सेट हैं? तीसरा आदेश निर्धारक बचाव के लिए आता है। हालांकि, इससे पहले कि मैं वेक्टर कला की गणना के लिए एल्गोरिदम पर आगे बढ़ने से पहले, मुझे एक छोटा गीतकार वापसी करना है।

यह पीछे हटना मूल वैक्टरों की चिंता करता है।

योजनाबद्ध रूप से, उन्हें चित्र में चित्रित किया गया है:

आप क्या सोचते हैं, उन्हें बुनियादी क्यों कहा जाता है? तथ्य यह है कि :

या तस्वीर में:

इस सूत्र का न्याय स्पष्ट है, क्योंकि:

वेक्टर कला

अब मैं एक वेक्टर के काम की शुरूआत के लिए आगे बढ़ सकता हूं:

दो वैक्टरों के वेक्टर उत्पाद को वेक्टर कहा जाता है जिसे निम्नलिखित नियम द्वारा गणना की जाती है:

अब चलो वेक्टर कला गणना के कुछ उदाहरण दें:

उदाहरण 1: वेक्टर वैक्टर खोजें:

समाधान: मैं निर्धारक बना देता हूं:

और इसकी गणना करें:

अब मूल वैक्टर के माध्यम से लिखने से, मैं वेक्टर की सामान्य रिकॉर्डिंग पर वापस आऊंगा:

इस तरह:

अब कोशिश करो।

तैयार? चेक:

और परंपरागत रूप से दो नियंत्रण के लिए कार्य:

1. वेक्टर क्लिप आर्ट खोजें:
2. वेक्टर क्लिप आर्ट खोजें:

उत्तर:

तीन वैक्टरों का मिश्रित उत्पाद

अंतिम डिजाइन जो मुझे आवश्यकता होगी वह तीन वैक्टरों का एक मिश्रित उत्पाद है। यह, साथ ही स्केलर, एक संख्या है। इसकी गणना करने के दो तरीके हैं। - निर्धारक के माध्यम से, एक मिश्रित काम के माध्यम से।

अर्थात्, हमें तीन संस्करण हैं:

फिर तीन वैक्टरों के मिश्रित उत्पाद की गणना की जा सकती है:

1. - यानी, एक मिश्रित उत्पाद दो अन्य वैक्टरों के वेक्टर उत्पाद पर एक वेक्टर का एक स्केलर उत्पाद है।

उदाहरण के लिए, तीन वैक्टरों का एक मिश्रित उत्पाद है:

स्वतंत्र रूप से एक वेक्टर उत्पाद के माध्यम से इसकी गणना करने का प्रयास करें और सुनिश्चित करें कि परिणाम मेल खाते हैं!

और फिर - आत्म समाधानों के लिए दो उदाहरण:

उत्तर:

समन्वय प्रणाली का चयन करें

खैर, अब हमारे पास ज्यामिति पर जटिल स्टीरियोमेट्रिक कार्यों को हल करने के लिए ज्ञान की सभी आवश्यक नींव है। हालांकि, अपने फैसले के उदाहरणों और एल्गोरिदम पर सीधे आगे बढ़ने से पहले, मेरा मानना \u200b\u200bहै कि यह अभी भी किस प्रश्न पर रोकना उपयोगी होगा: वास्तव में कैसे किसी विशेष आकृति के लिए समन्वय प्रणाली का चयन करें। आखिरकार, यह समन्वय प्रणाली के पारस्परिक स्थान की पसंद है और अंतरिक्ष में आकृति अंततः यह निर्धारित करेगी कि बोझिल गणना कैसे होगी।

मैं आपको याद दिलाता हूं कि इस खंड में हम निम्नलिखित आंकड़ों पर विचार करते हैं:

1. आयताकार समानांतर
2. प्रत्यक्ष प्रिज्म (त्रिकोणीय, हेक्सागोनल ...)
3. पिरामिड (त्रिकोणीय, चतुर्भुज)
4. टेट्राहेड्रॉन (एक और त्रिकोणीय पिरामिड के समान)

आयताकार समानांतरपिपेडा या घन के लिए, मैं अनुशंसा करता हूं कि आप निर्माण करें:

यही है, मैं "कोण में" रखूंगा। घन और समानांतर बहुत अच्छे आंकड़े हैं। उनके लिए, आप हमेशा अपने शिखर के निर्देशांक को आसानी से ढूंढ सकते हैं। उदाहरण के लिए, यदि (जैसा कि चित्र में दिखाया गया है)

शिखर के निर्देशांक निम्नानुसार हैं:

इसे याद रखने के लिए, निश्चित रूप से, यह याद रखने की आवश्यकता नहीं है कि घन या आयताकार समानांतर होना बेहतर कैसे है - अधिमानतः।

प्रत्यक्ष प्रिज्म

प्रिज्म एक अधिक हानिकारक आकृति है। अंतरिक्ष में स्थित यह अलग हो सकता है। हालांकि, मैं मुझे सबसे स्वीकार्य प्रतीत होता हूं:

त्रिकोणीय प्रिज्म:

यही है, त्रिभुज के किनारों में से एक जिसे हम पूरी तरह से धुरी पर डालते हैं, और एक शिखर में से एक निर्देशांक की शुरुआत के साथ मेल खाता है।

हेक्सागोनल प्रिज्म:

यही है, शिखर में से एक निर्देशांक की शुरुआत के साथ मेल खाता है, और पार्टियों में से एक एक्सिस पर स्थित है।

चतुर्भुज और हेक्सागोनल पिरामिड:

स्थिति, क्यूबा के समान: आधार के दो पक्ष हम समन्वय अक्षों के साथ गठबंधन करते हैं, जिसे हम समन्वय की शुरुआत के साथ जोड़ते हैं। एकमात्र मामूली जटिलता बिंदु के निर्देशांक की गणना करेगी।

हेक्सागोनल पिरामिड के लिए - समान रूप से एक हेक्सागोनल प्रिज्म के लिए। मुख्य कार्य फिर से वर्टेक्स के निर्देशांक की खोज में है।

टेट्राहेड्रॉन (त्रिकोणीय पिरामिड)

स्थिति उस व्यक्ति के समान ही है जिसे मैंने त्रिकोणीय प्रिज्म के लिए नेतृत्व किया था: एक चोटी निर्देशांक की शुरुआत के साथ मेल खाती है, एक तरफ समन्वय धुरी पर स्थित है।

खैर, अब हम अंततः समस्याओं को हल करने के करीब आने के करीब हैं। लेख की शुरुआत में मैंने जो कहा, आप इस निष्कर्ष को बना सकते हैं: अधिकांश सी 2 कार्य 2 श्रेणियों में विभाजित हैं: प्रति दूरी कोण और कार्यों में चुनौतियां। सबसे पहले, हम कोण खोजने के कार्यों पर विचार करेंगे। बदले में, उन्हें निम्नलिखित श्रेणियों में विभाजित किया गया है (जैसा कि जटिलता बढ़ जाती है):

कोनों को खोजने के लिए कार्य

1. दो सीधे के बीच कोण ढूँढना
2. दो विमानों के बीच कोण ढूँढना

आइए इन कार्यों पर लगातार विचार करें: चलिए दो सीधे के बीच कोण को ढूंढकर शुरू करते हैं। खैर, याद रखें, और क्या हमने पहले आपके समान उदाहरणों का फैसला किया था? मुझे याद है, क्योंकि हमारे पास ऐसा कुछ था ... हम दो वैक्टरों के बीच कोण की तलाश में थे। मैं आपको याद दिला दूंगा कि दो संस्करण दिए गए हैं: और, उनके बीच का कोने अनुपात से है:

अब हमारे पास एक लक्ष्य है - दो सीधे के बीच कोण ढूंढना। चलो "फ्लैट चित्र" की ओर मुड़ें:

कोनों ने दो सीधी रेखाओं के चौराहे के साथ कितना किया? पहले से ही टुकड़े। सच्चाई केवल दो से बराबर नहीं है, अन्य उनके लिए लंबवत हैं (और इसलिए वे उनके साथ मेल खाते हैं)। तो हमें किस तरह के कोण को दो सीधे के बीच कोण माना जाना चाहिए: या? यहां एक नियम है: दो प्रत्यक्ष के बीच कोण हमेशा डिग्री से अधिक नहीं। यही है, दो कोणों से, हम हमेशा सबसे छोटी डिग्री के साथ एक कोण चुनेंगे। यही है, इस तस्वीर में, दो के बीच कोण बराबर बराबर है। मॉड्यूल का उपयोग करने के लिए पेश किए गए दो कोणों में से सबसे छोटे कोणों की खोज के साथ परेशान न करें। इस प्रकार, दो प्रत्यक्ष के बीच कोण सूत्र द्वारा निर्धारित किया जाता है:

आप, एक सावधान पाठक की तरह, सवाल उठाना पड़ा: और वास्तव में, हम इन सबसे अधिक संख्याओं को ले लेंगे जो हमें कोने की कोसाइन की गणना करने की आवश्यकता है? उत्तर: हम उन्हें प्रत्यक्ष वैक्टर से ले जाएगा! इस प्रकार, दो सीधी रेखाओं के बीच कोण खोजने के लिए एल्गोरिदम निम्नानुसार है:

1. हम फॉर्मूला 1 लागू करते हैं।

या अधिक जानकारी में:

1. हम पहले प्रत्यक्ष के गाइड वेक्टर के निर्देशांक की तलाश में हैं
2. हम गाइड वेक्टर दूसरे प्रत्यक्ष के निर्देशांक की तलाश में हैं
3. उनके स्केलर उत्पाद के मॉड्यूल की गणना करें
4. पहले वेक्टर की लंबाई की तलाश में
5. दूसरे वेक्टर की लंबाई की तलाश में
6. पैराग्राफ 5 के परिणामों पर अनुच्छेद 4 के परिणामों को गुणा करें
7. हम खंड 6 के परिणामस्वरूप अनुच्छेद 3 के परिणाम को विभाजित करते हैं। हमें प्रत्यक्ष के बीच कोण का कोसाइन मिलता है
8. यदि यह परिणाम कोण की सटीक गणना करने की अनुमति देता है, तो हम इसकी तलाश कर रहे हैं
9. अन्यथा हम Arquosine के माध्यम से लिखते हैं

खैर, अब यह कार्यों में जाने का समय है: पहले दो का समाधान मैं विस्तार से प्रदर्शन करूंगा, मैं संक्षिप्त रूप में एक और निर्णय पेश करूंगा, और मैं केवल पिछले दो कार्यों के जवाब दूंगा, आपको सभी गणनाएं बितानी चाहिए उनको।

कार्य:

1. PRA-VILLE-NOME TET-RA-RA-REA-REA DI DI, CO.-CO-TET-RA-ed-RA और MEA-DI-BO-KO-COODINATES के बीच के कोने।

2. पीआरए-विले-नीयू-कोयला पीआई-आरए-एमआई-डी स्ट्रो-आरओ, ओएस-ना-विया बराबर हैं, और पसलियों का गुलदस्ता बराबर है, सीधे और के बीच कोने को।

3. पीआरए-विले चे-यू-राह-कोयला पीआई-आरए-एमआई की सभी पसलियों की लंबाई एक दूसरे के बराबर होती है। नाई-डी सीधा के बीच कोण और यदि से-re-zok - सह-अकेले दिया गया पीआई-आरए-एमआई-डीडब्ल्यूआई, बिंदु उसके गुलदस्ते पसली पर se-re-di-di- पर है

4. मेरे प्रति बिंदु से घन के किनारे पर ताकि नाई-डी को कोने सीधे और

5. प्वाइंट - सी-री-डी-ऑन किनार्स क्यूबा नाई-डी सीधे और के बीच कोने।

मैंने इस क्रम में कार्यों को गलत समझा। जबकि आपके पास समन्वय विधि में नेविगेट शुरू करने का समय नहीं है, मैं खुद को सबसे अधिक "समस्या" आंकड़ों को अलग करता हूं, और आप आपको सबसे सरल घन से निपटने के लिए देंगे! धीरे-धीरे, आपको सभी आंकड़ों के साथ काम करना सीखना होगा, कार्यों की जटिलता मैं विषय से विषय तक बढ़ेगा।

हम समस्याओं को हल करने के लिए आगे बढ़ते हैं:

1. एक टेट्राहेड्रॉन बनाएं, इसे समन्वय प्रणाली में रखें क्योंकि मैंने पहले डिज़ाइन किया था। चूंकि टेट्राफेड सही है - फिर इसके सभी चेहरे (बेस सहित) - सही त्रिकोण। चूंकि हमें पक्ष की लंबाई नहीं दी जाती है, तो मैं इसे बराबर ले सकता हूं। मुझे लगता है कि आप समझते हैं कि कोण वास्तव में इस बात पर निर्भर नहीं करेगा कि हमारे टेट्राहेड्रॉन कैसे "खिंचाव" करेंगे? टेट्राहेड्रा ऊंचाई और मध्यस्थ में भी खर्च करें। रास्ते में, मैं इसके आधार को पेंट करता हूं (यह भी आसान होगा)।

मुझे के बीच कोण खोजने की जरूरत है। हम क्या जानते हैं? हम केवल बिंदु समन्वय जानते हैं। इसलिए, अंक के अधिक निर्देशांक खोजने के लिए आवश्यक है। अब हम सोचते हैं: बिंदु त्रिभुज के ऊंचाई (या बिसेट्रिस या औसत) के चौराहे का बिंदु है। और बिंदु एक उठा हुआ बिंदु है। बिंदु खंड का मध्य है। फिर हम निश्चित रूप से खोजने की ज़रूरत है: अंक के निर्देशांक :.

आइए सबसे सरल के साथ शुरू करें: बिंदु के निर्देशांक। आकृति को देखें: यह स्पष्ट है कि बिंदु का बिंदु शून्य है (बिंदु विमान पर स्थित है)। उसका आदेश (चूंकि मध्य) के बराबर है। यह Abscissa खोजने के लिए कठिन है। हालांकि, यह आसानी से पाइथागोरा प्रमेय के आधार पर किया जाता है: एक त्रिकोण पर विचार करें। इसका हाइपोटेन्यूज बराबर है, और कैथेट में से एक बराबर है:

अंत में हमारे पास है :.

अब हम बिंदु के निर्देशांक पाते हैं। यह स्पष्ट है कि उसका ऐप्लिकेट फिर से शून्य है, और इसकी अधीनता बिंदु के समान ही है, यानी। उसे Abscissa खोजें। यह हमेशा किया जाता है, अगर आपको याद है चौराहे बिंदु के समतुल्य त्रिभुज की ऊंचाई अनुपात में विभाजित होती है, शीर्ष से गिनती। चूंकि:, तब सेगमेंट की लंबाई के बराबर वांछित एब्सिसा बिंदु बराबर है :. इस प्रकार, बिंदु के निर्देशांक बराबर हैं:

बिंदु के निर्देशांक का पता लगाएं। यह स्पष्ट है कि इसका एब्रिसा और ऑर्डिनेट Abscissa और सामान्य बिंदु के साथ मेल खाता है। और आवेदक सेगमेंट की लंबाई के बराबर है। - यह त्रिभुज के कैथियों में से एक है। त्रिभुज hypotenuse एक कट-कैट है। वह उन कारणों की तलाश में है जो मैंने एक बोल्ड पर प्रकाश डाला है:

बिंदु खंड का मध्य है। फिर हमें सेगमेंट के बीच के निर्देशांक के सूत्र को याद रखने की आवश्यकता है:

खैर, सब, अब हम गाइड वैक्टर के निर्देशांक खोज सकते हैं:

खैर, सब कुछ तैयार है: हम सूत्र में सभी डेटा को प्रतिस्थापित करते हैं:

इस तरह,

उत्तर:

आपको इस तरह के "डरावनी" उत्तर डराया नहीं जाना चाहिए: कार्यों के लिए सी 2 सामान्य अभ्यास है। मैं इस भाग में "सुंदर" उत्तर को आश्चर्यचकित करूंगा। इसके अलावा, जैसा कि आपने उल्लेख किया है, मैंने व्यावहारिक रूप से पाइथागोरो प्रमेय और समतुल्य त्रिभुज ऊंचाई की संपत्ति को छोड़कर कुछ भी नहीं किया। यही है, स्टीरियोमीटर कार्य को हल करने के लिए, मैंने न्यूनतम स्टीरियोमेट्री का उपयोग किया। इस आंशिक रूप से "क्वेंचिंग" में जीत काफी भारी कंप्यूटिंग है। लेकिन वे एल्गोरिदम पर्याप्त हैं!

2. मैं समन्वय प्रणाली के साथ-साथ इसके आधार के साथ सही हेक्सागोनल पिरामिड दिखाऊंगा:

हमें सीधे और के बीच कोण खोजने की जरूरत है। इस प्रकार, हमारे कार्य को बिंदुओं के निर्देशांक की खोज में कम कर दिया गया है :. पिछले तीन के निर्देशांक हम एक छोटे से पैटर्न पर पाएंगे, और हम बिंदु समन्वय के माध्यम से शिखर के समन्वय को पाएंगे। थोक में काम करता है, लेकिन आपको इसे शुरू करने की जरूरत है!

ए) समन्वय: यह स्पष्ट है कि इसकी आवेदक और ordinate शून्य के बराबर हैं। हमें Abscissa मिलता है। ऐसा करने के लिए, एक आयताकार त्रिकोण पर विचार करें। हां, हम केवल hypotenuse द्वारा जाना जाता है, जो बराबर है। देखो हम खोजने की कोशिश करेंगे (क्योंकि यह स्पष्ट है कि श्रेणी की दोगुनी लंबाई हमें एक फरार बिंदु देगी)। हम उसकी तलाश कैसे करते हैं? आइए याद रखें कि आंकड़े के लिए हम पिरामिड के आधार पर झूठ बोलते हैं? यह सही हेक्सागोन है। इसका क्या मतलब है? इसका मतलब है कि उसके पास सभी पार्टियां हैं और सभी कोनों के बराबर हैं। ऐसे कोण को ढूंढना आवश्यक होगा। कोई विचार? विचार द्रव्यमान, लेकिन एक सूत्र है:

सही एन-संसद के कोनों का योग बराबर है .

इस प्रकार, सही हेक्सागोन के कोणों का योग डिग्री के बराबर है। फिर प्रत्येक कोने के बराबर है:

हम फिर से तस्वीर को देखते हैं। यह स्पष्ट है कि कट-बिसेक्टर कोण। फिर कोण डिग्री के बराबर है। फिर:

फिर, जहां से।

इस प्रकार, निर्देशांक है

बी) अब आप आसानी से बिंदु समन्वय कर सकते हैं :.

सी) हम बिंदु के निर्देशांक पाएंगे। चूंकि इसका एब्रिसा सेगमेंट की लंबाई के साथ मेल खाता है, यह बराबर है। आदेश को ढूंढना बहुत मुश्किल नहीं है: यदि हम अंकों को जोड़ते हैं और प्रत्यक्ष पदनाम के चौराहे का एक बिंदु, मान लेते हैं। (एक साधारण निर्माण खुद बनाओ)। फिर इस प्रकार, ऑर्डिनेट पॉइंट बी सेगमेंट की लंबाई के बराबर है। त्रिकोण के लिए फिर से बारी। फिर

फिर क्योंकि तब बिंदु का समन्वय होता है

डी) अब हम बिंदु के निर्देशांक पाएंगे। एक आयताकार पर विचार करें और साबित करें कि बिंदु निर्देशांक:

ई) यह शिखर के निर्देशांक को खोजने के लिए बनी हुई है। यह स्पष्ट है कि इसका एब्सिसा और ऑर्डिनेट Abscissa और सामान्य बिंदु के साथ मेल खाता है। हम आवेदक को पाते हैं। तब से। एक आयताकार त्रिकोण पर विचार करें। समस्या की स्थिति से, पार्श्व किनारे। यह मेरे त्रिकोण का हाइपोटिनस है। फिर पिरामिड की ऊंचाई - Catat।

फिर बिंदु निर्देशांक है:

खैर, सब कुछ, मेरे पास मेरे लिए ब्याज के सभी बिंदुओं के निर्देशांक हैं। मैं प्रत्यक्ष के प्रत्यक्ष वैक्टर के निर्देशांक की तलाश में हूं:

हम इन वैक्टरों के बीच एक कोण की तलाश में हैं:

उत्तर:

दोबारा, इस कार्य को हल करते समय, मैंने सही एन-वर्ग के कोनों की मात्रा के रूप में, साथ ही आयताकार त्रिभुज की साइन की परिभाषा को छोड़कर किसी भी अनियमित तकनीकों का उपयोग नहीं किया था।

3. चूंकि हमें फिर से पिरामिड में पसलियों की लंबाई नहीं दी जाती है, तो मैं उन्हें एक के बराबर मानूंगा। इस प्रकार, चूंकि सभी पसलियों, न केवल पक्ष, एक दूसरे के बराबर होते हैं, फिर पिरामिड के आधार पर और वर्ग झूठ बोल रहा है, और साइड चेहरे सही त्रिभुज हैं। हम इस पिरामिड के साथ-साथ विमान पर इसके आधार को दिखाएंगे, कार्य के पाठ में दिए गए सभी डेटा को ध्यान में रखते हुए:

हम के बीच कोण की तलाश में हैं और। जब मैं अंक के निर्देशांक की खोज करता हूं तो मैं बहुत छोटी गणना करूंगा। आपको उन्हें "समझने" की आवश्यकता होगी:

बी) - सेगमेंट के बीच में। इसके निर्देशांक:

सी) कटौती की लंबाई मैं त्रिभुज में पायथागोरा प्रमेय पर पाऊंगा। मैं त्रिभुज में पाइथागोरियन प्रमेय पर पाऊंगा।

निर्देशांक:

डी) - सेगमेंट का एमआईडीटी। इसके निर्देशांक बराबर हैं

ई) वेक्टर निर्देशांक

एफ) वेक्टर निर्देशांक

जी) हम एक कोण की तलाश में हैं:

घन सबसे सरल आंकड़ा है। मुझे यकीन है कि आप अपने आप से निपटेंगे। कार्यों के उत्तर 4 और 5 निम्नानुसार हैं:

सीधे और विमान के बीच कोण ढूँढना

खैर, सरल कार्यों का समय खत्म हो गया है! अब उदाहरण और भी मुश्किल होंगे। सीधे और विमान के बीच कोने को खोजने के लिए, हम निम्नानुसार होंगे:

1. तीन बिंदुओं से हम एक विमान समीकरण का निर्माण करते हैं
   ,
   तीसरे क्रम के निर्धारक का उपयोग करना।
2. दो बिंदुओं से हम एक प्रत्यक्ष गाइड निर्देशांक की तलाश में हैं:
3. हम सीधे और विमान के बीच कोण की गणना के लिए सूत्र का उपयोग करते हैं:

जैसा कि आप देख सकते हैं, यह सूत्र इस तथ्य के समान ही है कि हम दो सीधे के बीच कोनों की खोज करते थे। सही भाग की संरचना केवल वही है, और अब हम अब साइनस की तलाश में हैं, और पहले की तरह कोसाइन नहीं करते हैं। खैर, एक विपरीत कार्रवाई को जोड़ा गया - विमान के समीकरण की खोज।

चलो एक लंबे बॉक्स में स्थगित नहीं है उदाहरण का समाधान:

1. ओएस-नो-वीए-नी-यह एक सीधी खरीद-गोद-बेन-एसएमटीए शरारती-ना-डी-री-कोयला उपनाम है - आप-एक पुरस्कार बराबर है। नाय-डायन-सी-सेंट के बीच कोने

2. प्रत्यक्ष-मो-एमआर में। पीए-राल-लेस-ले-पीआई-डी-डी-डाई नाय-डी-लेवल कॉर्नर से सीधे और फ्लैट-सह के बीच -

3. प्रा-विले में, गर्दन-कोयला पुरस्कार-अल्टो सभी पसलियों बराबर होते हैं। नाई-डी कोने सीधे और फ्लैट-सह-सेंट के बीच कोने।

4. ओएस-नो-वीए नी-वेस्ट-ना-डी-चोर के साथ पीआरए-विले ट्रे-कोयला पीआई-आरए-एमआई-डी में, ओबरा-ज़ो-वान ओएस-नो की एक फ्लैट-सह-सह-प्रतिलिपि- वीए और सीधे, प्रो-हो-बेटा री-डी पसलियों के माध्यम से और

5. PRA-VIL-OTE चार-जन्मे पीआई-आरए-एमआई-डीई की सभी पसलियों की लंबाई एक दूसरे के बराबर होती है। नाय-डी कोण सीधे और फ्लैट-सह-स्टू के बीच कोण यदि बिंदु सी-री-डी-ऑन-सह-सह-रिब पी-आरए-एमआई-डीई है।

फिर, मैं पहले दो कार्यों को विस्तार से तय करूंगा, तीसरा - संक्षेप में, और अंतिम दो आपको एक स्वतंत्र निर्णय के लिए छोड़ देंगे। इसके अलावा, आपको पहले से ही त्रिकोणीय और चतुर्भुज पिरामिड से निपटना पड़ता है, लेकिन प्रिज्म के साथ - अब तक कोई नहीं है।

समाधान:

1. एक प्रिज्म के साथ ही इसके आधार को दिखाएं। यह समन्वय प्रणाली के साथ संगत है और टेर्क स्थिति में दिए गए सभी डेटा को नोट करता है:

मैं अनुपात के साथ कुछ अनुपालन के लिए क्षमा चाहता हूं, लेकिन समस्या को हल करने के लिए, यह अनिवार्य रूप से इतना महत्वपूर्ण नहीं है। विमान बस मेरे प्रिज्म की "पिछली दीवार" है। यह अनुमान लगाने के लिए पर्याप्त है कि इस तरह के विमान का समीकरण है:

हालांकि, इसे सीधे दिखाया जा सकता है:

इस विमान पर मनमाने ढंग से तीन अंक चुनें: उदाहरण के लिए,।

एक विमान समीकरण बनाओ:

आप के लिए व्यायाम: स्वतंत्र रूप से इस निर्धारक की गणना करें। क्या आप सफल हुए? फिर विमान का समीकरण है:

या केवल

इस तरह,

उदाहरण को हल करने के लिए, मुझे सीधे वेक्टर के निर्देशांक को सीधे ढूंढने की आवश्यकता है। चूंकि बिंदु निर्देशांक की शुरुआत के साथ गिर गया है, इसलिए वेक्टर निर्देशांक बस इस बिंदु के निर्देशांक के साथ मेल खाते हैं, इसलिए हम बिंदु के निर्देशांक की शुरुआत में पाएंगे।

ऐसा करने के लिए, एक त्रिकोण पर विचार करें। हम शीर्ष से ऊंचाई (यह औसत और द्विभाजक) खर्च करेंगे। चूंकि, ऑर्डिनेट पॉइंट बराबर है। इस बिंदु के Abscissa को खोजने के लिए, हमें सेगमेंट की लंबाई की गणना करने की आवश्यकता है। पाइथागोरा प्रमेय के अनुसार, हमारे पास है:

फिर बिंदु निर्देशांक है:

बिंदु को "उठाया गया" बिंदु पर:

फिर वेक्टर के निर्देशांक:

उत्तर:

जैसा कि आप देख सकते हैं, ऐसे कार्यों को हल करने में मौलिक रूप से कुछ भी मुश्किल नहीं है। वास्तव में, प्रक्रिया प्रिज्म के रूप में "सीधे" इस तरह के आंकड़े को सरल बनाती है। अब चलिए निम्नलिखित उदाहरण पर जाएं:

2. एक समानांतरपाइप तैयार करें, हम एक विमान और प्रत्यक्ष करते हैं, साथ ही साथ इसके निचले आधार को अलग-अलग आकर्षित करते हैं:

सबसे पहले हम विमान समीकरण पाते हैं: इसमें तीन बिंदुओं के निर्देशांक:

(पहले दो निर्देशांक एक स्पष्ट तरीके से प्राप्त किए जाते हैं, और अंतिम समन्वय आप आसानी से बिंदु से चित्र ढूंढ सकते हैं)। फिर विमान के समीकरण का गठन:

गणना:

हम गाइड वेक्टर के निर्देशांक की तलाश में हैं: यह स्पष्ट है कि इसके निर्देशांक बिंदु के निर्देशांक के साथ मेल खाते हैं, है ना? निर्देशांक कैसे खोजें? यह प्रति इकाई एप्लिकेट अक्ष के साथ उठाए गए बिंदु के निर्देशांक हैं! । फिर वांछित कोण की तलाश करें:

उत्तर:

3. सही हेक्सागोनल पिरामिड रखो, और फिर विमान और प्रत्यक्ष खर्च करें।

एक समस्या को आकर्षित करने के लिए एक विमान भी है, इस कार्य के समाधान का उल्लेख न करें, हालांकि, समन्वय विधि अभी भी है! यह उसकी बहुमुखी प्रतिभा में है और इसका मुख्य लाभ है!

विमान तीन अंक से गुजरता है :. हम उनके निर्देशांक की तलाश में हैं:

एक) । पिछले दो बिंदुओं के लिए खुद को आउटपुट निर्देशांक। आप एक हेक्सागोनल पिरामिड के साथ चुनौती के लिए इस समाधान के लिए उपयोगी होंगे!

2) हम विमान के समीकरण का निर्माण करते हैं:

हम वेक्टर के निर्देशांक की तलाश में हैं :. (फिर से त्रिकोणीय पिरामिड के साथ कार्य देखें!)

3) हम एक कोण की तलाश में हैं:

उत्तर:

जैसा कि आप देख सकते हैं, इन कार्यों में कुछ भी अलौकिक नहीं है। जड़ों के साथ बहुत सावधान रहना आवश्यक है। पिछले दो कार्यों के लिए मैं केवल उत्तर दूंगा:

आप कैसे सुनिश्चित कर सकते हैं कि हर जगह कार्यों को हल करने की तकनीक: मुख्य कार्य कोने के निर्देशांक को खोजने और उन्हें कुछ सूत्रों में प्रतिस्थापित करने के लिए। हम कोनों की गणना के लिए चुनौतियों के एक और वर्ग पर विचार करने के लिए छोड़ दिया, अर्थात्:

दो विमानों के बीच कोणों की गणना

एल्गोरिदम समाधान होंगे:

1. तीन बिंदुओं के लिए हम पहले विमान के समीकरण की तलाश में हैं:
2. अन्य तीन बिंदुओं के लिए हम दूसरे विमान के समीकरण की तलाश में हैं:
3. हम सूत्र का उपयोग करते हैं:

जैसा कि आप देख सकते हैं, सूत्र पिछले दो के समान ही है, जिसके साथ हमने सीधे और विमान के बीच कोनों को खोजा। तो याद रखें कि आपको बहुत कठिनाई नहीं होगी। हम तुरंत कार्यों के विश्लेषण पर जाते हैं:

1. एसटी-आरओ-ओएस-नो-विल-वीआईएल-विल्टर ट्रे-कंसाइड क्यूस्यूज कहां है, और डी-हॉल बो-को-को-कॉप बराबर है। एफ-सी-स्टू और एफ-सह-स्टू ओएस-नो-विया पुरस्कार के बीच कोण नाय-डी कोण-हम।

2. प्रा-विले-मील-देह-कोयला पीआई-आरए-एमआई-डी में, सभी पसलियां बराबर होती हैं, एफ-सह-स्टू और सह-स्टू के बीच कोने का साइनस, पेन के माध्यम से प्रो-हो-फिथ -पेन-डी-लीयर पेन-डी-लीयर, लेकिन सीधे।

3. एसटी-आरओ-यूएस के सही चे-द-कोयले-कोयले पुरस्कार में, ओएस-ना-वाया बराबर है, और किनारों का गुलदस्ता बराबर है। मेरे किनारे पर - बिंदु पर ताकि। फ्लैट-को-मील और के बीच कोण का पता लगाएं

4. पीआरए-विलियन चार-जन्मे पुरस्कार-हमारे में, ओएस-ना-वाया बराबर है, और बौ-वे रिब्रा बराबर है। एक बिंदु के किनारे पर ताकि फ्लैट-को-एमआई के बीच नाई-डी कोने और।

5. क्यूबा में, फ्लैट-सह-स्टी के बीच नऊ-डी को-सी-नस कोण और

कार्य समाधान:

1. सही वृद्धि (आधार पर एक समतुल्य त्रिभुज है) एक त्रिभुज प्रिज्म और इस विमान पर ध्यान दें जो समस्या की स्थिति में दिखाई देते हैं:

हमें दो विमानों के समीकरणों को खोजने की आवश्यकता है: आधार समीकरण तुच्छ प्राप्त किया जाता है: आप तीन बिंदुओं के लिए उचित निर्धारक बना सकते हैं, मैं तुरंत समीकरण का गठन करूंगा:

अब हम पाएंगे कि बिंदु समीकरण में बिंदु के निर्देशांक हैं - क्योंकि यह मध्ययुगीन और त्रिभुज की ऊंचाई है, यह आसानी से त्रिभुज में पायथागोरा प्रमेय पर स्थित है। फिर बिंदु के निर्देशांक हैं: इसके लिए आवेदन बिंदु एक आयताकार त्रिभुज पर विचार करें

फिर हम इन निर्देशांक प्राप्त करते हैं: हम विमान के समीकरण को लिखेंगे।

विमानों के बीच कोण की गणना करें:

उत्तर:

2. ड्राइंग बनाओ:

सबसे मुश्किल बात यह समझना है कि यह एक रहस्यमय विमान है जो बिंदु के माध्यम से लंबवत रूप से गुजर रहा है। खैर, मुख्य बात यह है कि? मुख्य बात चौकसता है! वास्तव में, प्रत्यक्ष लंबवत है। सीधे लंबवत भी है। फिर इन दो सीधी रेखाओं के माध्यम से गुजरने वाला विमान सीधे के लिए लंबवत होगा, और वैसे, बिंदु के माध्यम से गुजरता है। यह विमान भी पिरामिड के शीर्ष से गुजरता है। फिर वांछित विमान - और विमान हमें पहले से ही दिया गया है। हम अंक के निर्देशांक की तलाश में हैं।

बिंदु के समन्वय बिंदु के माध्यम से मिलेगा। एक छोटी सी ड्राइंग से यह निकालना आसान है कि बिंदु के निर्देशांक इस तरह होंगे: पिरामिड की चोटी के निर्देशांक को खोजने के लिए अब क्या बचा है? आपको अभी भी इसकी ऊंचाई की गणना करने की आवश्यकता है। यह उसी पायथागोर के प्रमेय की मदद से किया जाता है: पहले साबित करें कि (छोटे त्रिभुजों की पुरानी रूप से, आधार पर एक वर्ग बनाने)। शर्त के तहत, हमारे पास है:

अब सब कुछ तैयार है: शिखर के निर्देशांक:

एक विमान समीकरण बनाओ:

आप निर्धारकों की गणना में पहले से ही विशेष हैं। मुश्किल के बिना, आपको मिलेगा:

या अन्यथा (यदि दोनों की जड़ के लिए दोनों भाग हैं)

अब हम विमान के समीकरण पाते हैं:

(आप यह नहीं भूलते कि हम विमान के समीकरण कैसे प्राप्त करते हैं, हालांकि? यदि आप समझ में नहीं आते हैं कि यह शून्य से कहां से आया है, फिर विमान के समीकरण की परिभाषा पर वापस आएं! बस हमेशा इससे पहले कि यह पता चला मेरा विमान निर्देशांक की शुरुआत से संबंधित था!)

निर्धारक की गणना करें:

(आप ध्यान दे सकते हैं कि विमान के समीकरण सीधे अंक के माध्यम से सीधे गुजरने के समीकरण के साथ मेल खाते थे! सोचो क्यों!)

अब हम कोण की गणना करते हैं:

हमें साइनस खोजने की भी आवश्यकता है:

उत्तर:

3. Caverny प्रश्न: एक आयताकार प्रिज्म क्या है, आप क्या सोचते हैं? यह सिर्फ एक विशेष रूप से प्रसिद्ध समानांतर है! तुरंत ड्राइंग करें! आप भी अलग-अलग आधार को चित्रित नहीं कर सकते हैं, इसके लाभ यहां थोड़ा सा है:

विमान, जैसा कि हमने पहले ही पहले से देखा है, समीकरण के रूप में लिखा गया है:

अब एक विमान बनाओ

समीकरण विमान का समीकरण है:

हम एक कोण की तलाश में हैं:

अब पिछले दो कार्यों के जवाब:

खैर, अब यह थोड़ा आराम करने का समय है, क्योंकि हम बहुत अच्छे हैं और आपने एक बड़ी नौकरी की है!

निर्देशांक और वैक्टर। उन्नत स्तर, उच्च स्तर

इस लेख में हम आपके साथ एक और वर्ग के साथ चर्चा करेंगे जिन्हें समन्वय विधि का उपयोग करके हल किया जा सकता है: दूरी की गणना के लिए कार्य। अर्थात्, हम निम्नलिखित मामलों पर विचार करेंगे:

1. सीधे क्रॉस-कंट्री के बीच की दूरी की गणना।

मैंने इन कार्यों को आदेश दिया क्योंकि उनकी जटिलता बढ़ जाती है। सबसे सिर्फ खोजने के लिए बाहर निकलता है बिंदु से विमान की दूरीऔर सबसे कठिन बात यह है कि खोजने के लिए क्रॉस-कंट्री के बीच की दूरी सीधे। हालांकि, निश्चित रूप से, कुछ भी असंभव नहीं है! आइए एक लंबे बॉक्स में स्थगित न हों और तुरंत कार्यों की प्रथम श्रेणी पर विचार करने के लिए आगे बढ़ें:

बिंदु से विमान तक की दूरी की गणना

इस कार्य को हल करने के लिए हमें क्या चाहिए?

1. बिंदु के निर्देशांक

इसलिए, जैसे ही हमें सभी आवश्यक डेटा मिलते हैं, हम सूत्र का उपयोग करते हैं:

चूंकि हम विमान के समीकरण का निर्माण करते हैं, आपको पहले से ही पिछले भाग में समझा जाने वाला पिछले कार्यों से जाना जाना चाहिए। आइए तुरंत कार्यों के लिए आगे बढ़ें। यह योजना निम्नानुसार है: 1, 2 - मैं आपको निर्णय लेने में मदद करता हूं, और काफी विस्तार, 3, 4 - केवल उत्तर, निर्णय जो आप खर्च करते हैं और तुलना करते हैं। शुरू कर दिया है!

कार्य:

1. दान क्यूब। घन की धार की लंबाई बराबर है। सी-डी-डी से फ्लैट-सह-सेंट तक नाई डी-चोर

2. दाना Pra-Vil-Naya Che-Mi-ya-coal-naya pi-mi-da boe-co-co-rib stro-ro-ro-ro-ro-ro-hia बराबर है। नाय-डी-कि बिंदु से फ्लैट-सह-अल्पविराम तक sto-yast - Se-Re-Di-Ribs पर।

3. पीआरए-विले ट्रे-कोयला पीआई-आरए-एमआई-डी में ओएस-नो-वीए-नी-को-सीओ-वे समान रूप से, और एक सौ-आरओ-ऑन ओएस-एनए के बराबर है। वे-शि-शिई से नाई डी-चोर-हम फ्लैट-सीओ-सेंट के लिए।

4. पीआरए-विले सीम-कोयले पुरस्कार-अकेले में, सभी रिब्रा बराबर है। नाय-डी-उस बिंदु से फ्लैट-सह-सेंट तक।

समाधान:

1. एकल किनारों के साथ एक घन खींचें, हम एक सेगमेंट और एक विमान बनाते हैं, सेगमेंट के बीच में हम पत्र को इंगित करते हैं

.

सबसे पहले, चलो फेफड़ों से शुरू करते हैं: बिंदु के निर्देशांक को ढूंढें। इसके बाद से (सेगमेंट के बीच के निर्देशांक याद रखें!)

अब हम तीन-बिंदु विमान के समीकरण को संकलित करते हैं

\\ [\\ Left | (\\ _ प्रारंभ (सरणी) (* (20) (c)) x & 0 & 1 \\\\ y & 1 & 0 \\\\ z & 1 & 1 \\ end (सरणी)) \\ राइट | \u003d 0 \\]

अब मैं दूरी की खोज के लिए आगे बढ़ सकता हूं:

2. हम फिर से ड्राइंग से शुरू करते हैं, जहां हम सभी डेटा मनाते हैं!

पिरामिड के लिए यह अपने आधार को खींचने के लिए अलग से उपयोगी होगा।

यहां तक \u200b\u200bकि तथ्य यह भी कि मैं एक चिकन पंजा के रूप में पेंट करता हूं, इस कार्य को हल करने के लिए हमें आसानी से नहीं रोकता है!

अब बिंदु निर्देशांक ढूंढना आसान है

बिंदु के निर्देशांक के रूप में, तो

2. चूंकि बिंदु ए - सेगमेंट के बीच के निर्देशांक, फिर

विमान के समीकरण को बनाने और इसे सरल बनाने के लिए हमें विमान पर दो और अंक के निर्देशांक भी मिलते हैं:

\\ [\\ Left | (\\ Left | (\\ BEGIN (सरणी) (* (20) (c)) x & 1 & (\\ frac (3) (2)) \\\\ y & 0 & (\\ frac (3) (2)) \\ \\ Z & 0 & (\\ frac ((\\ sqrt 3)) (2)) \\ END (सरणी)) \\ दाएं |) \\ राइट | \u003d 0 \\]

चूंकि बिंदु निर्देशांक है: फिर हम दूरी की गणना करते हैं:

उत्तर (बहुत दुर्लभ!):

खैर, पता लगाया? ऐसा लगता है कि सब कुछ तकनीकी रूप से उन उदाहरणों में भी है जो हमने पिछले भाग में आपके साथ विचार किया है। तो मुझे यकीन है कि यदि आपने सामग्री को महारत हासिल कर ली है, तो आपको शेष दो कार्यों को हल करना मुश्किल नहीं होगा। मैं केवल जवाब दूंगा:

सीधे विमान से दूरी की गणना

वास्तव में, यहां कुछ भी नया नहीं है। एक दूसरे के सापेक्ष सीधे और विमान कैसे स्थित हो सकता है? उनके पास सभी संभावनाएं हैं: क्रॉस, या सीधे विमान के समानांतर। आप क्या सोचते हैं, एक सीधी रेखा से विमान के बराबर दूरी जिसके साथ यह प्रत्यक्ष अंतर होता है? ऐसा लगता है कि यह स्पष्ट है कि दूरी शून्य है। अनिच्छुक मामला।

दूसरा मामला चालाक है: दूरी पहले से ही नॉनज़रो है। हालांकि, सीधे समानांतर विमान के बाद से, प्रत्येक बिंदु इस विमान के बराबर है:

इस तरह:

इसका मतलब यह है कि मेरा कार्य पिछले एक के लिए ड्रिल किया गया था: हम सीधे लाइन पर किसी भी बिंदु के निर्देशांक की तलाश में हैं, हम विमान के समीकरण की तलाश करते हैं, बिंदु से विमान तक की दूरी की गणना करते हैं। वास्तव में, परीक्षा में ऐसे कार्य बेहद दुर्लभ हैं। मैं केवल एक कार्य खोजने में कामयाब रहा, और इसमें डेटा ऐसा था कि समन्वय विधि बहुत अधिक लागू नहीं हुई थी!

हम अब दूसरे को बदलते हैं, कार्यों की एक और अधिक महत्वपूर्ण वर्ग:

दूरी बिंदु की गणना प्रत्यक्ष करने के लिए

हमें क्या जरूरत है?

1. उस बिंदु के निर्देशांक जिनसे हम दूरी की तलाश में हैं:

2. लाइन पर झूठ बोलने वाले किसी भी बिंदु के निर्देशांक

3. प्रत्यक्ष वैक्टर प्रत्यक्ष निर्देशांक

किस फॉर्मूला?

इस अंश के denominator आपके लिए क्या मतलब है और इसलिए यह स्पष्ट होना चाहिए: यह गाइड वेक्टर की लंबाई सीधे है। यहाँ एक बहुत ही चालाक संख्या है! अभिव्यक्ति का अर्थ वैक्टर के वेक्टर उत्पाद का मॉड्यूल (लंबाई) है और वेक्टर के काम की गणना कैसे करें, हमें काम के पिछले हिस्से में अध्ययन किया गया था। अपने ज्ञान को अपडेट करें, अब वे हमारे लिए बहुत उपयोगी होंगे!

इस प्रकार, एल्गोरिदम हल करने में समस्या निम्न होगी:

1. हम उस बिंदु के निर्देशांक की तलाश में हैं जिससे हम दूरी की तलाश में हैं:

2. हम लाइन पर किसी भी बिंदु के निर्देशांक की तलाश में हैं, जिसे हम दूरी की तलाश में हैं:

3. वेक्टर बनाएं

4. लाइन गाइड वेक्टर का निर्माण

5. वेक्टर कला की गणना करें

6. हम परिणामी वेक्टर की लंबाई की तलाश में हैं:

7. दूरी की गणना करें:

हमारे पास बहुत काम है, और उदाहरण काफी जटिल होंगे! तो अब सभी ध्यान केंद्रित करें!

1. दाना प्रिया-विल-नया ट्रे-कोयला-नया पाई-आरए-एमआई-हां शब्द-शिह के साथ। वन-आरओ-ऑन ओएस-नो-विया पी-आरए-एमआई-डीया बराबर है, आप समान हैं। एसई डी-डी-केओ-सीओ-रिब से सीधे, जहां अंक और - री-डी पसलियों और सह-से-वीट-डाउन से नाई डी-चोर।

2. पसलियों और प्रत्यक्ष-एम-कोयले-लेकिन-गोवा पैराले-ले-ली-पीआई-हां की लंबाई सह-से-वाहनों के बराबर होती है - लेकिन वे-शि-रे से नाई-डी-चोर भी डायरेक्ट

3. पीआरए-विले सीम-कोयले पुरस्कार-अकेले में, सभी पसलियां नाई-डी-चोर मार्ग के बराबर बिंदु तक सीधे होती हैं

समाधान:

1. एक साफ ड्राइंग बनाएं, जो सभी डेटा को चिह्नित करता है:

हमारे पास आपके साथ बहुत काम है! मैं पहले उन शब्दों का वर्णन करना चाहूंगा जिन्हें हम देखेंगे और किस क्रम में:

1. अंक के निर्देशांक और

2. बिंदु के निर्देशांक

3. अंक के निर्देशांक और

4. वैक्टर के निर्देशांक और

5. उनकी वेक्टर कला

6. वेक्टर की लंबाई

7. वेक्टर की लंबाई लंबाई

8. से दूरी

खैर, हमारे पास बहुत काम है! हम उसके लिए स्वीकार कर रहे हैं, आस्तीनों को डरावने!

1. पिरामिड ऊंचाई के निर्देशांक को खोजने के लिए, हमें शून्य के बराबर आवेदक के बिंदु के निर्देशांक को जानने की आवश्यकता है, और ordinate के abscissa के बराबर है की ऊंचाई के बाद से सेगमेंट की लंबाई के बराबर है समतुल्य त्रिभुज, फिर यह रिश्ते में बांटा गया है, शीर्ष से गिनती है, इसलिए। अंत में, उन्हें निर्देशांक प्राप्त हुए:

बिंदु के निर्देशांक

2. - मध्य कट

3. - मिड सेगमेंट

मध्य कटौती

4.copinates

वेक्टर के निर्देशांक

5. वेक्टर कला की गणना करें:

6. वेक्टर की लंबाई: सबसे आसान तरीका यह है कि सेगमेंट त्रिभुज की मध्य रेखा है, जिसका अर्थ है कि यह आधार के बराबर है। इसलिए कि।

7. हम वेक्टर के काम की लंबाई पर विचार करते हैं:

8. अंत में, हमें दूरी मिलती है:

यूवी, ठीक है! ईमानदारी से, मैं कहूंगा: पारंपरिक तरीकों (निर्माण के माध्यम से) के साथ इस समस्या का समाधान बहुत तेज होगा। लेकिन यहां मैं सभी को समाप्त एल्गोरिदम में कम कर दिया! तो मुझे लगता है कि एल्गोरिदम आपके लिए स्पष्ट है? इसलिए, मैं आपको शेष दो कार्यों को हल करने के लिए कहूंगा। उत्तर की तुलना करें?

फिर, मैं दोहराता हूं: निर्माण के माध्यम से हल करने के लिए ये कार्य आसान (तेज़) होते हैं, और समन्वय विधि का सहारा नहीं लेते हैं। मैंने केवल एक सार्वभौमिक विधि दिखाने के लिए निर्णय के इस तरह के समाधान का प्रदर्शन किया जो आपको कुछ भी पकड़ने की अनुमति देता है। "

अंत में, कार्यों के अंतिम वर्ग पर विचार करें:

क्रॉस-कंट्री के बीच की दूरी की गणना

यहां, कार्यों को हल करने के लिए एल्गोरिदम पिछले एक के समान होगा। हमारे पास क्या है:

3. किसी भी वेक्टर कनेक्टिंग अंक पहले और दूसरे सीधे:

हम सीधे के बीच की दूरी की तलाश में कैसे हैं?

सूत्र निम्नानुसार है:

न्यूमरेटर एक मिश्रित उत्पाद का एक मॉड्यूल है (हमें पिछले भाग में प्रशासित किया गया था), और denominator पिछले सूत्र (प्रत्यक्ष वैक्टर के वेक्टर उत्पाद के मॉड्यूल, प्रत्यक्ष वैक्टर के मॉड्यूल, जिसके बीच हम देख रहे हैं) ।

मैं आपको याद दिलाऊंगा

तब फिर दूरी के लिए सूत्र को रूप में फिर से लिखा जा सकता है:

निर्धारक साझा करने के लिए एकल निर्धारक! हालांकि, ईमानदार होने के लिए, मैं बिल्कुल मजाक नहीं कर रहा हूँ! वास्तव में यह सूत्र बहुत बोझिल है और पर्याप्त जटिल गणना की ओर जाता है। आपके स्थान पर, मैं केवल सबसे चरम मामले में इसका सहारा लेगा!

आइए ऊपर उल्लिखित विधि का उपयोग करके कई कार्यों को हल करने का प्रयास करें:

1. पीआरई-विले, ट्रे-कोयले पुरस्कार में, सभी रिब्र को-रॉय बराबर हैं, नाई डी-सीधे के उन rourour।

2. दाना-विल-नया ट्रे-कोयला-नया इनाम-एमए सभी रिब ओएस-नो-वे-वे एसई-मानव, प्रो-हो-दादा के बराबर है, जो बो-सह-शोक के माध्यम से किनारे और se-re- di जावा-लुए-ज़िया क्वद-रा-टॉम की पसलियों है। Riats और के बीच nay-di-thes rostozhone

मैं पहले हल करता हूं, और उस पर भरोसा करता हूं, आप दूसरा तय करते हैं!

1. मैं एक प्रिज्म खींचता हूं और सीधे मार्क करता हूं और

बिंदु के निर्देशांक सी: फिर

बिंदु के निर्देशांक

वेक्टर के निर्देशांक

बिंदु के निर्देशांक

वेक्टर के निर्देशांक

वेक्टर के निर्देशांक

\\ [\\ Left ((b, \\ overrightarrow (a (a_1)) \\ overrightarrow (b (b_1))) \\ राइट) \u003d \\ Left | (\\ BEGIN (सरणी) (* (20) (l)) (\\ BEGIN (सरणी) (* (20) (c)) 0 & 1 & 0 अंत (सरणी)) \\\\ (\\ BEGIN (सरणी) (* (20) (c)) 0 & 0 & 1 \\ end (सरणी)) \\\\ (\\ _ शुरू (सरणी) (* (20) (c)) (\\ frac ((\\ sqrt 3)) (2)) & (- \\ frac (1) (2)) और 1 \\ end (सरणी)) \\ अंत (सरणी)) \\ अधिकार | \u003d \\ Frac ((\\ sqrt 3)) (2) \\]

हम वेक्टर के बीच वेक्टर उत्पाद पर विचार करते हैं और

\\ [\\ Overrightarrow (a (a_1)) \\ cdot \\ overrightarrow (b (c_1)) \u003d \\ Left | \\ BEGIN (सरणी) (l) \\ _ शुरू (* (20) (c)) (\\ overrightarrow i) & (\\ overightarrow j) & (\\ overightarrow k) \\ end (सरणी) \\\\\\ शुरू (सरणी) ) (* (20) (सी)) 0 और 0 और 1 \\ END (ARRAY) \\\\\\ BEGIN (* (20) (c)) (\\ frac ((\\ sqrt 3)) (2)) & (- \\ frac (1) (2)) और 1 \\ end (सरणी) \\ अंत (सरणी) \\ अधिकार | - \\ frac ((\\ sqrt 3)) (2) \\ overrightarrow k + \\ frac (1) (2) \\ overrightarrow i \\]

अब हम इसे एक लंबाई मानते हैं:

उत्तर:

अब दूसरे कार्य को सटीक रूप से पूरा करने का प्रयास करें। इसका जवाब होगा :.

निर्देशांक और वैक्टर। संक्षिप्त विवरण और मूल सूत्र

वेक्टर - दिशात्मक कट। - वेक्टर की शुरुआत, - सामग्री वेक्टर।
वेक्टर को दर्शाया गया है या।

निरपेक्ष मूल्यवेक्टर - कटौती की लंबाई वेक्टर को दर्शाती है। के रूप में भेजा।

वेक्टर के निर्देशांक:

,
जहां - वेक्टर \\ displaystyle के सिरों।

वैक्टर का योग :.

वैक्टर बनाना:

वैक्टर का स्केलर उत्पाद: