Užduotys, kurių sprendimas yra transformacija logaritmines išraiškas , yra gana dažni vieningo valstybinio egzamino metu.

Norint sėkmingai su jomis susidoroti su minimaliu laiku, be pagrindinių logaritminių tapatybių, reikia žinoti ir teisingai naudoti dar keletą formulių.

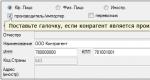
Tai yra: a log a b = b, kur a, b > 0, a ≠ 1 (Tai tiesiogiai išplaukia iš logaritmo apibrėžimo).

log a b = log c b / log c a arba log a b = 1/log b a
kur a, b, c > 0; a, c ≠ 1.

log a m b n = (m/n) log |a| |b|
kur a, b > 0, a ≠ 1, m, n Є R, n ≠ 0.

a log c b = b log c a
kur a, b, c > 0 ir a, b, c ≠ 1

Norėdami parodyti ketvirtosios lygybės galiojimą, paimkime kairės ir dešinės pusės logaritmą į bazę a. Gauname rąstas a (a rąstas su b) = log a (b log su a) arba rąstas su b = rąstas su a · log a b; log c b = log c a · (log c b / log c a); log su b = rąstas su b.

Mes įrodėme logaritmų lygybę, o tai reiškia, kad išraiškos pagal logaritmus taip pat yra lygios. Formulė 4 buvo įrodyta.

1 pavyzdys.

Apskaičiuokite 81 log 27 5 log 5 4 .

Sprendimas.

81 = 3 4 , 27 = 3 3 .

log 27 5 = 1/3 log 3 5, log 5 4 = log 3 4 / log 3 5. Todėl

log 27 5 log 5 4 = 1/3 log 3 5 (log 3 4 / log 3 5) = 1/3 log 3 4.

Tada 81 log 27 5 log 5 4 = (3 4) 1/3 log 3 4 = (3 log 3 4) 4/3 = (4) 4/3 = 4 3 √4.

Toliau pateiktą užduotį galite atlikti patys.

Apskaičiuokite (8 log 2 3 + 3 1/ log 2 3) - log 0,2 5.

Kaip užuomina, 0,2 = 1/5 = 5 -1 ; log 0,2 5 = -1.

Atsakymas: 5.

2 pavyzdys.

Apskaičiuoti (√11) žurnalas √3 9- log 121 81 .

Sprendimas.

Pakeiskime išraiškas: 9 = 3 2, √3 = 3 1/2, log √3 9 = 4,

121 = 11 2, 81 = 3 4, log 121 81 = 2 log 11 3 (naudojama 3 formulė).

Tada (√11) log √3 9- log 121 81 = (11 1/2) 4-2 log 11 3 = (11) 2- log 11 3 = 11 2 / (11) log 11 3 = 11 2 / ( 11 log 11 3) = 121/3.

3 pavyzdys.

Apskaičiuokite log 2 24 / log 96 2 - log 2 192 / log 12 2.

Sprendimas.

Pavyzdyje esančius logaritmus pakeičiame logaritmais su 2 baze.

log 96 2 = 1/log 2 96 = 1/log 2 (2 5 3) = 1/(log 2 2 5 + log 2 3) = 1/(5 + log 2 3);

log 2 192 = log 2 (2 6 3) = (log 2 2 6 + log 2 3) = (6 + log 2 3);

log 2 24 = log 2 (2 3 3) = (log 2 2 3 + log 2 3) = (3 + log 2 3);

log 12 2 = 1/log 2 12 = 1/log 2 (2 2 3) = 1/(log 2 2 2 + log 2 3) = 1/(2 + log 2 3).

Tada log 2 24 / log 96 2 – log 2 192 / log 12 2 = (3 + log 2 3) / (1/(5 + log 2 3)) – ((6 + log 2 3) / (1/( 2 + log 2 3)) =

= (3 + log 2 3) · (5 + log 2 3) – (6 + log 2 3) (2 + log 2 3).

Atidarę skliaustus ir atvedę panašius terminus, gauname skaičių 3. (Supaprastindami reiškinį, log 2 3 galime žymėti n ir supaprastinti išraišką

(3 + n) · (5 + n) – (6 + n)(2 + n)).

Atsakymas: 3.

Galite patys atlikti šią užduotį:

Apskaičiuoti (log 3 4 + log 4 3 + 2) log 3 16 log 2 144 3.

Čia reikia pereiti prie 3 bazinių logaritmų ir didelių skaičių faktorizavimo į pirminius veiksnius.

Atsakymas: 1/2

4 pavyzdys.

Duoti trys skaičiai A = 1/(log 3 0,5), B = 1/(log 0,5 3), C = log 0,5 12 – log 0,5 3. Išdėstykite juos didėjančia tvarka.

Sprendimas.

Transformuokime skaičius A = 1/(log 3 0,5) = log 0,5 3; C = log 0,5 12 – log 0,5 3 = log 0,5 12/3 = log 0,5 4 = -2.

Palyginkime juos

log 0,5 3 > log 0,5 4 = -2 ir log 0,5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.

Arba -2< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.

Atsakymas. Todėl skaičių išdėstymo tvarka: C; A; IN.

5 pavyzdys.

Kiek sveikųjų skaičių yra intervale (log 3 1 / 16 ; log 2 6 48).

Sprendimas.

Nustatykime, tarp kurių skaičiaus 3 laipsnių yra skaičius 1/16. Gauname 1/27< 1 / 16 < 1 / 9 .

Kadangi funkcija y = log 3 x didėja, tada log 3 (1/27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.

log 6 48 = log 6 (36 4 / 3) = log 6 36 + log 6 (4 / 3) = 2 + log 6 (4 / 3). Palyginkime žurnalą 6 (4/3) ir 1/5. Ir tam mes lyginame skaičius 4/3 ir 6 1/5. Pakelkime abu skaičius iki 5 laipsnio. Gauname (4/3) 5 = 1024 / 243 = 4 52 / 243< 6. Следовательно,

6 žurnalas (4/3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.

Todėl intervalas (log 3 1 / 16; log 6 48) apima intervalą [-2; 4] ir ant jo dedami sveikieji skaičiai -2; -1; 0; 1; 2; 3; 4.

Atsakymas: 7 sveikieji skaičiai.

6 pavyzdys.

Apskaičiuokite 3 lglg 2/ lg 3 - lg20.

Sprendimas.

3 lg lg 2/ lg 3 = (3 1/ lg3) lg lg 2 = (3 lо g 3 10) lg lg 2 = 10 lg lg 2 = lg2.

Tada 3 lglg2/lg3 - lg 20 = lg 2 – lg 20 = lg 0,1 = -1.

Atsakymas: -1.

7 pavyzdys.

Yra žinoma, kad log 2 (√3 + 1) + log 2 (√6 – 2) = A. Raskite log 2 (√3 –1) + log 2 (√6 + 2).

Sprendimas.

Skaičiai (√3 + 1) ir (√3 – 1); (√6 – 2) ir (√6 + 2) yra konjuguoti.

Atlikime tokią išraiškų transformaciją

√3 – 1 = (√3 – 1) · (√3 + 1)) / (√3 + 1) = 2/(√3 + 1);

√6 + 2 = (√6 + 2) · (√6 – 2)) / (√6 – 2) = 2/(√6 – 2).

Tada log 2 (√3 – 1) + log 2 (√6 + 2) = log 2 (2/(√3 + 1)) + log 2 (2/(√6 – 2)) =

Log 2 2 – log 2 (√3 + 1) + log 2 2 – log 2 (√6 – 2) = 1 – log 2 (√3 + 1) + 1 – log 2 (√6 – 2) =

2 – log 2 (√3 + 1) – log 2 (√6 – 2) = 2 – A.

Atsakymas: 2 – A.

8 pavyzdys.

Supaprastinkite ir suraskite apytikslę išraiškos reikšmę (log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9.

Sprendimas.

Sumažinkime visus logaritmus iki bendros bazės 10.

(log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9 = (lg 2 / lg 3) (lg 3 / lg 4) (lg 4 / lg 5) (lg 5 / lg 6) · … · (lg 8 / lg 9) · lg 9 = lg 2 ≈ 0,3010 (Apytikslę lg 2 reikšmę galima rasti naudojant lentelę, skaidrės taisyklę arba skaičiuotuvą).

Atsakymas: 0,3010.

9 pavyzdys.

Apskaičiuokite log a 2 b 3 √(a 11 b -3), jei log √ a b 3 = 1. (Šiame pavyzdyje a 2 b 3 yra logaritmo pagrindas).

Sprendimas.

Jei log √ a b 3 = 1, tai 3/(0,5 log a b = 1. Ir log a b = 1/6.

Tada log a 2 b 3√(a 11 b -3) = 1/2 log a 2 b 3 (a 11 b -3) = log a (a 11 b -3) / (2log a (a 2 b 3) ) = (log a a 11 + log a b -3) / (2(log a a 2 + log a b 3)) = (11 – 3log a b) / (2(2 + 3log a b)) Atsižvelgiant į tai, kad tas log a b = 1/ 6 gauname (11 – 3 1/6) / (2(2 + 3 1/6)) = 10,5/5 = 2,1.

Atsakymas: 2.1.

Galite patys atlikti šią užduotį:

Apskaičiuokite log √3 6 √2,1, jei log 0,7 27 = a.

Atsakymas: (3 + a) / (3a).

10 pavyzdys.

Apskaičiuokite 6,5 4/ log 3 169 · 3 1/ log 4 13 + log125.

Sprendimas.

6,5 4/ log 3 169 · 3 1/ log 4 13 + log 125 = (13/2) 4/2 log 3 13 · 3 2/ log 2 13 + 2 log 5 5 3 = (13/2) 2 log 13 3 3 2 log 13 2 + 6 = (13 log 13 3 / 2 log 13 3) 2 (3 log 13 2) 2 + 6 = (3/2 log 13 3) 2 (3 log 13 2) 2 + 6 = ( 3 2 /(2 log 13 3) 2) · (2 ​​log 13 3) 2 + 6.

(2 log 13 3 = 3 log 13 2 (4 formulė))

Gauname 9 + 6 = 15.

Atsakymas: 15.

Vis dar turite klausimų? Nežinote, kaip rasti logaritminės išraiškos reikšmę?
Norėdami gauti pagalbos iš dėstytojo, užsiregistruokite.
Pirma pamoka nemokama!

svetainėje, kopijuojant visą medžiagą ar jos dalį, būtina nuoroda į šaltinį.

Logaritminės išraiškos, sprendimų pavyzdžiai. Šiame straipsnyje apžvelgsime problemas, susijusias su logaritmų sprendimu. Užduotyse keliamas klausimas, kaip rasti posakio prasmę. Pažymėtina, kad logaritmo sąvoka naudojama daugelyje užduočių ir jos prasmės supratimas yra nepaprastai svarbus. Kalbant apie vieningą valstybinį egzaminą, logaritmas naudojamas sprendžiant lygtis, atliekant taikomuosius uždavinius, taip pat atliekant užduotis, susijusias su funkcijų tyrimu.

Pateiksime pavyzdžių, kad suprastume pačią logaritmo reikšmę:

Pagrindinė logaritminė tapatybė:

Logaritmų savybės, kurias visada reikia atsiminti:

*Darbos logaritmas lygus faktorių logaritmų sumai.

* * *

*Dalyvio (trupmens) logaritmas lygus faktorių logaritmų skirtumui.

* * *

*Laipsnio logaritmas lygus eksponento sandaugai ir jo bazės logaritmui.

* * *

*Perėjimas prie naujų pamatų

* * *

Daugiau savybių:

* * *

Logaritmų skaičiavimas yra glaudžiai susijęs su eksponentų savybių naudojimu.

Išvardinkime kai kuriuos iš jų:

Šios savybės esmė ta, kad skaitiklį perkėlus į vardiklį ir atvirkščiai, rodiklio ženklas pasikeičia į priešingą. Pavyzdžiui:

Šios nuosavybės pasekmė:

* * *

Didinant laipsnį į laipsnį, bazė išlieka ta pati, tačiau rodikliai dauginami.

* * *

Kaip matėte, pati logaritmo sąvoka yra paprasta. Svarbiausia, kad jums reikia geros praktikos, kuri suteikia jums tam tikrų įgūdžių. Žinoma, reikia žinoti formules. Jei įgūdis konvertuoti elementarius logaritmus nebuvo išugdytas, tada spręsdami paprastas užduotis galite lengvai suklysti.

Praktikuokite, pirmiausia išspręskite paprasčiausius matematikos kurso pavyzdžius, tada pereikite prie sudėtingesnių. Ateityje tikrai parodysiu, kaip išsprendžiami „baisūs“ logaritmai, jie nepasirodys vieningame valstybiniame egzamine, bet jie yra įdomūs, nepraleiskite jų!

Tai viskas! Sėkmės tau!

Pagarbiai Aleksandras Krutitskichas

P.S. Būčiau dėkingas, jei papasakotumėte apie svetainę socialiniuose tinkluose.

EGOROVA VIKTORIJA VALERIEVNA

Matematikos mokytojas

aukščiausia kvalifikacinė kategorija

TEMA: „IDENTALI TRANSFORMACIJA

LOGARITMINĖS IŠRAIKOS"

Žinios ir įgūdžiai, kuriuos studentai turėtų įgyti baigę studijas šią pamoką:

žinoti skaičiaus logaritmo apibrėžimą, pagrindinį logaritminį tapatumą, logaritmų savybes;

mokėti atlikti logaritmus turinčių reiškinių transformacijas ir skaičiuoti logaritmus.

Literatūra:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. ir kt. Algebra ir analizės pradžia: vadovėlis 10-11 klasėms ugdymo įstaigose. – M.: Švietimas, 2001.

2. Kochagin V.V., Kochagina M.V., Intensyvus pasirengimo vieningam valstybiniam egzaminui kursas. – M.: Eksmo, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Algebrinis simuliatorius: vadovas moksleiviams ir pareiškėjams. – M.: Ilexa, 2005 m.

4. Gusevas V.A., Mordkovičius A.G. Matematika: Pamatinės medžiagos: Knyga studentams. – M.: Švietimas, 2001.

Pamokos planas:

Pamokos eiga:

1) Logaritmas yra graikiškas žodis, susidedantis iš 2 žodžių: „logos“ – santykis, „aritmos“ – skaičius. Tai reiškia, kad logaritmas yra skaičius, matuojantis santykį. 1614 m. publikacija pranešė, kad Napier išrado logaritmus. Vėliau jis sudarė logaritmines lenteles, kurios dabar mums žinomos kaip Bradis lentelės. Mažiau nei per šimtmetį lentelės išplito visame pasaulyje ir tapo nepakeičiamu skaičiavimo įrankiu. Vėliau jie buvo tarsi įmontuoti į patogų įrenginį, kuris labai pagreitina skaičiavimo procesą - skaidrių taisyklę, kuri buvo naudojama iki XX amžiaus aštuntojo dešimtmečio.

1 priedas.

2) Logaritmas teigiamas skaičiusb remiantis a, ir A didesnis už nulį ir nelygu vienam,yra rodiklis, iki kurio turi būti padidintas skaičiusa norėdami gauti numerįb.

Ši lygybė, išreiškianti logaritmo apibrėžimą, vadinamapagrindinė logaritminė tapatybė .

C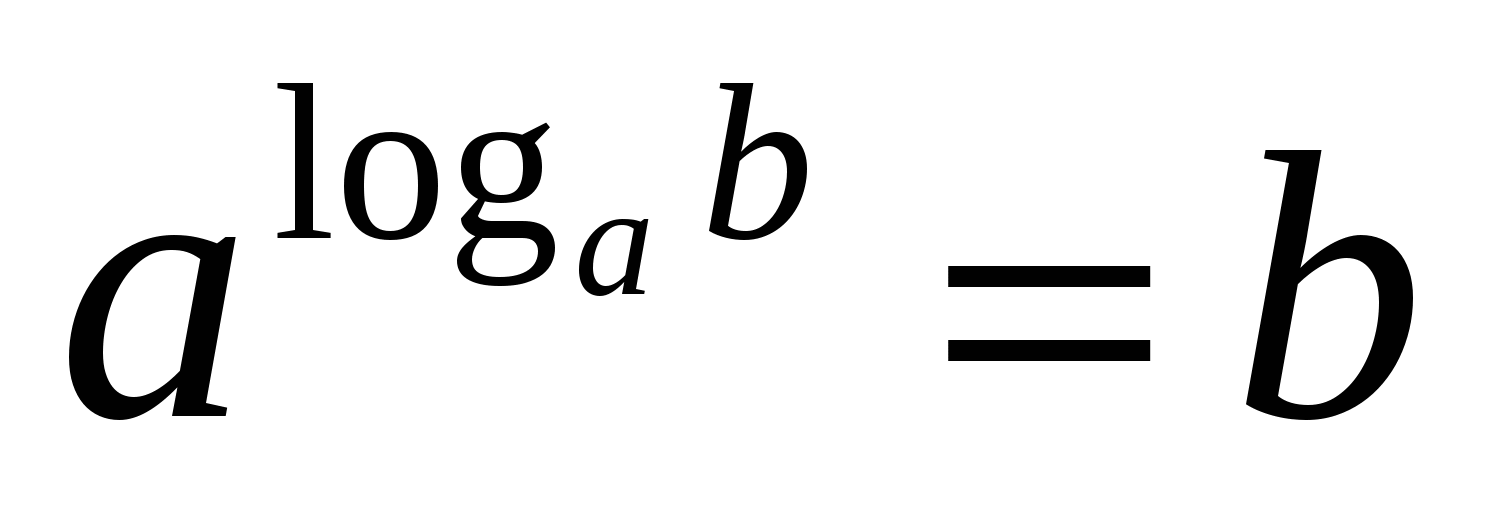

ARBA 1

P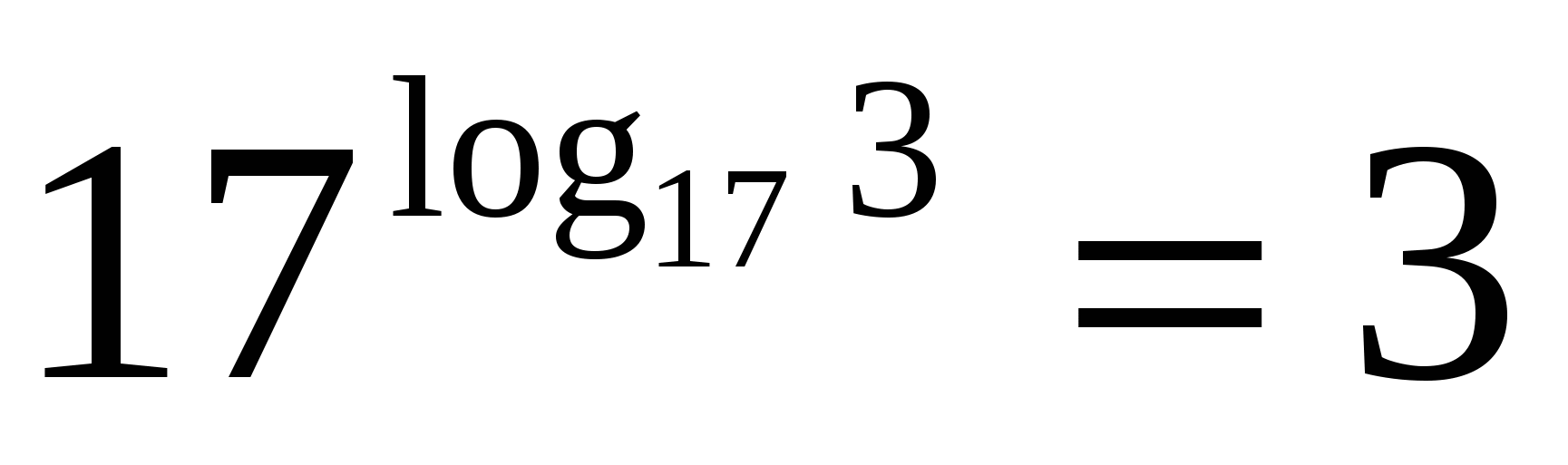

Laipsnio bazė ir logaritmo bazė yra septyniolika, o tai reiškia, kad pagal pagrindinę logaritminę tapatybę išraiškos reikšmė yra trys.

Dirbkime žodžiu:

SCH
FIR-BELLE

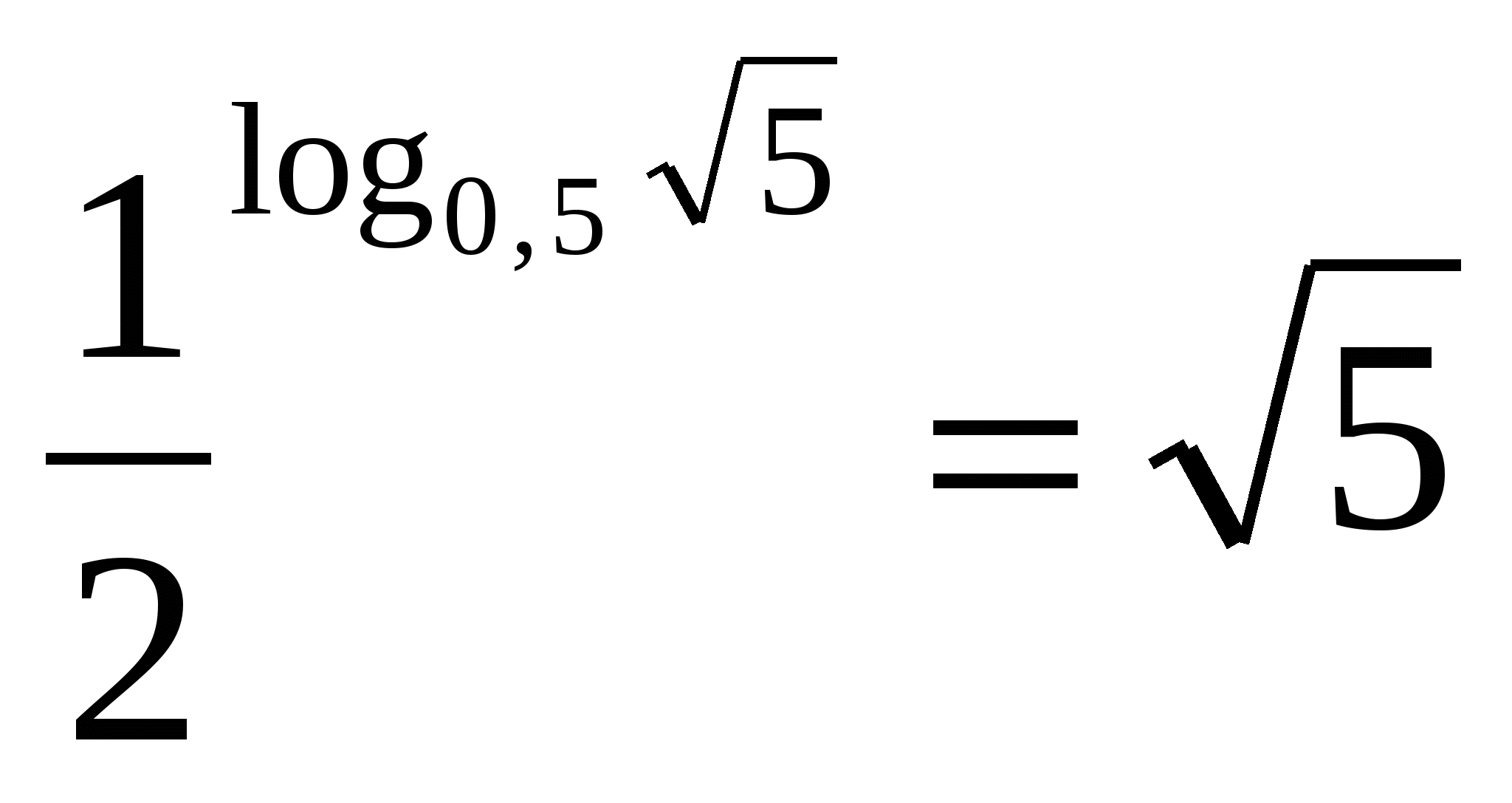
APIE antrojo apačia lygi nuliui taškui penki, o tai reiškia, kad išraiška yra lygi aritmetikai kvadratinė šaknis iš penkių.

P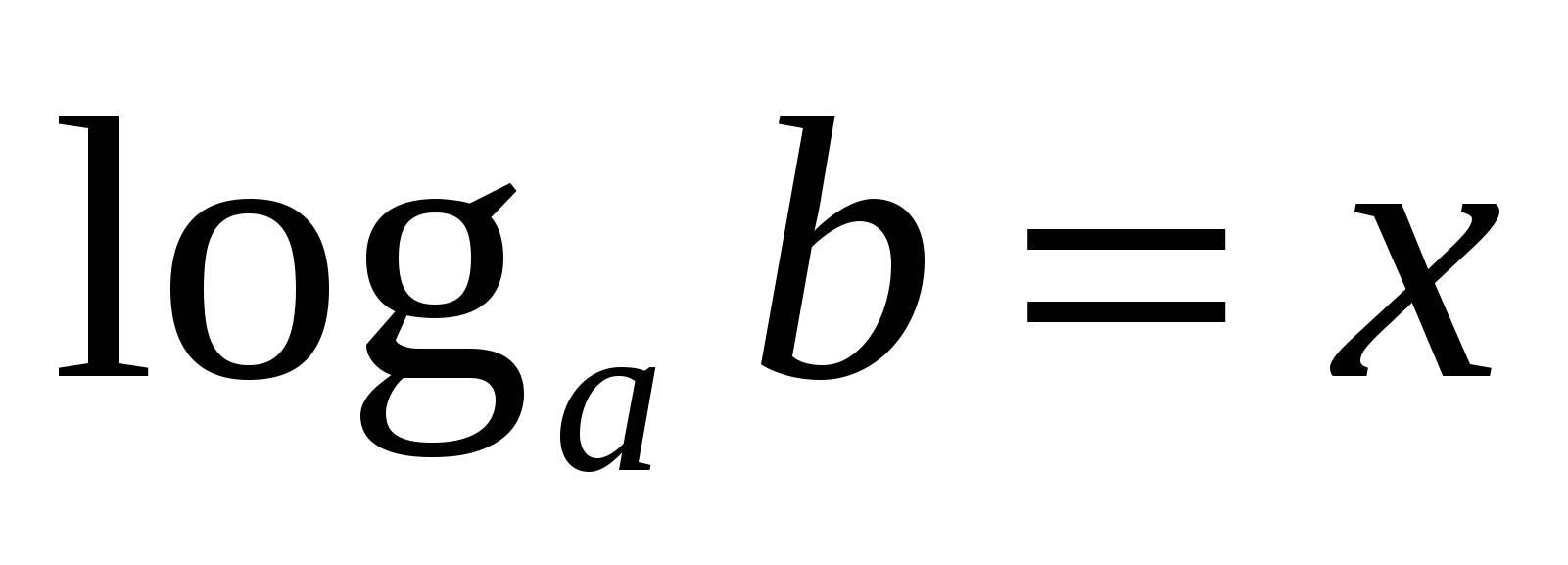

2 priedas.

Lygybė reiškia tai

Iš logaritmo apibrėžimo gaunamos šios svarbios lygybės:

Pavyzdžiui:

P
3 priedas.

Pereikime prie Vieningų valstybinių egzaminų užduotys:

4 priedas.

3
) Yra specialus dešimties bazinio logaritmo žymėjimas ir pavadinimasdešimtainis logaritmas .

L
bazinis kalibrase paskambinonatūralusis logaritmas .

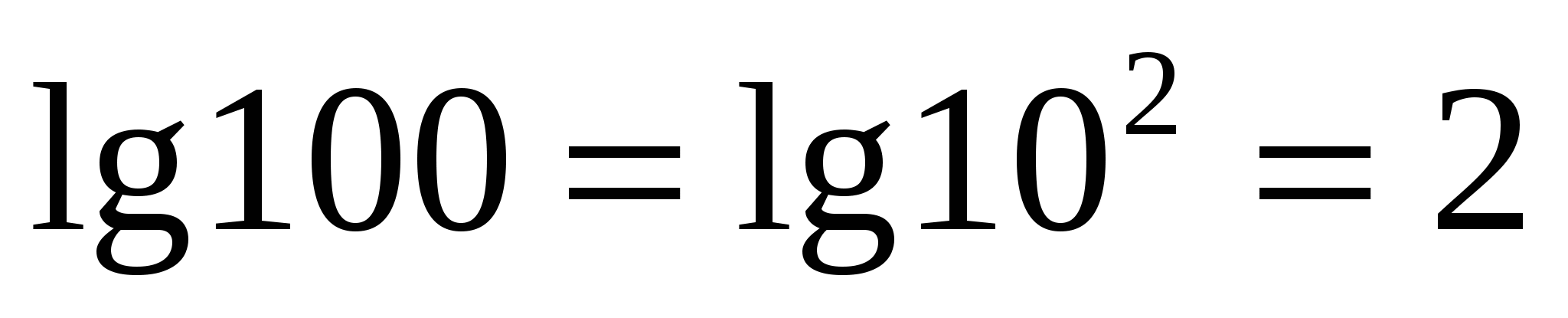
N
pavyzdžiui,

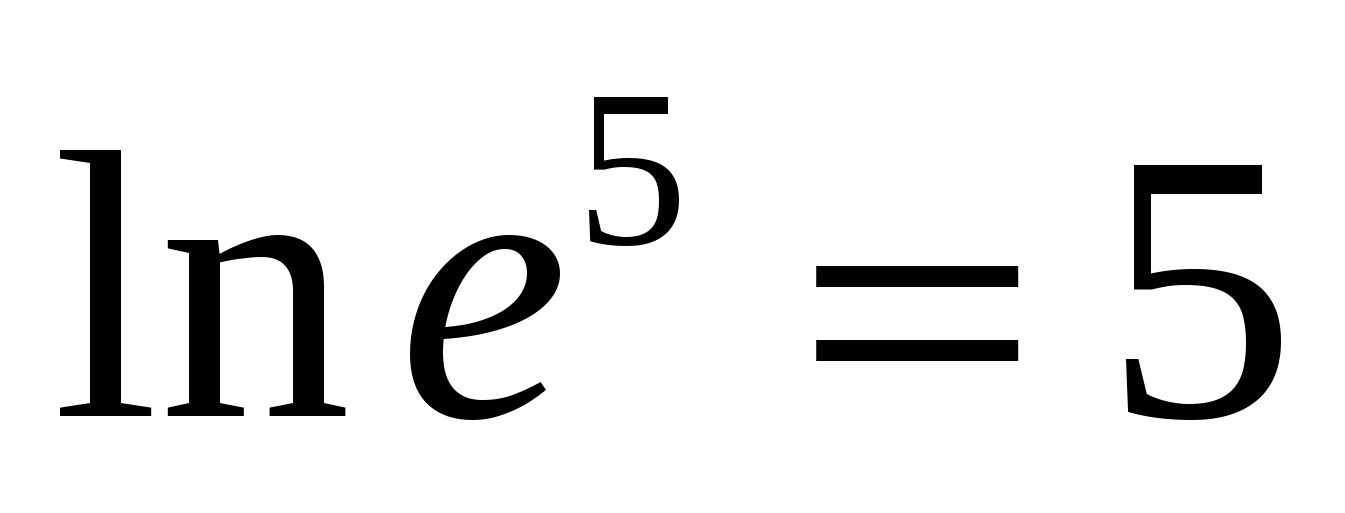
4) Šios savybės išplaukia iš logaritmo apibrėžimo. Visos savybės yra suformuluotos ir įrodytos tik teigiamas vertes kintamieji, esantys po logaritminiais ženklais.

Dviejų teigiamų skaičių sandaugos iki pagrindo logaritmas A lygus šių skaičių logaritmų sumai su ta pačia baze.

TsOR 2

Pavyzdžiui,

Z
1 užduotis.

2 užduotis. Supaprastinkite išraišką

IN
Naudokime ankstesnio pavyzdžio sprendimą. Mes pakeisime

Atkreipkite dėmesį, kad logaritmas yra kvadratas, todėl suma turi būti pakelta kvadratu. Naudodami sumos kvadrato formulę, atidarome skliaustus. Pateiksime panašius terminus.

5) Dalinio logaritmas lygus dividendo ir daliklio logaritmų skirtumui.

C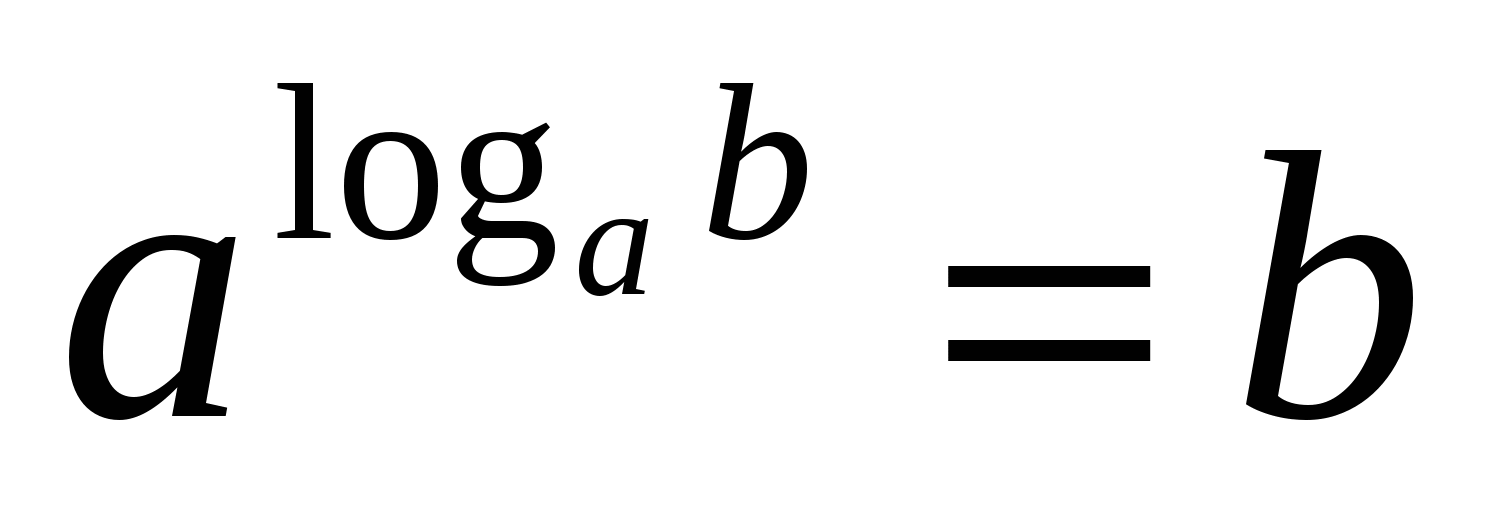

Atkreipkite dėmesį į galios pagrindą ir logaritmo pagrindą - jie yra vienodi.

ARBA 3

R

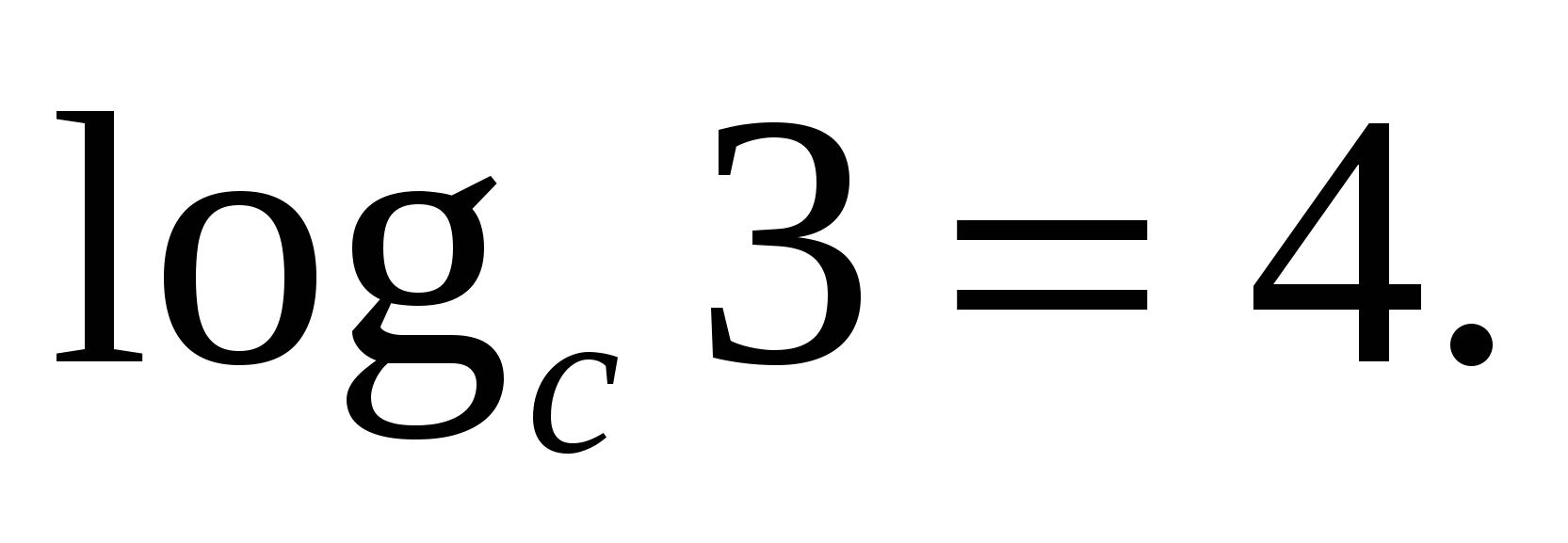Pažvelkime į šios formulės taikymą naudodami pavyzdį:

Z
1 užduotis. Raskite išraiškos reikšmę if

2 užduotis. Raskite vertę b pagal jo logaritmą

6) Laipsnio logaritmas į bazęA , yra lygus eksponento ir logaritmo sandaugai, naudojant tą pačią bazę.

TsOR 4

Pavyzdžiui,

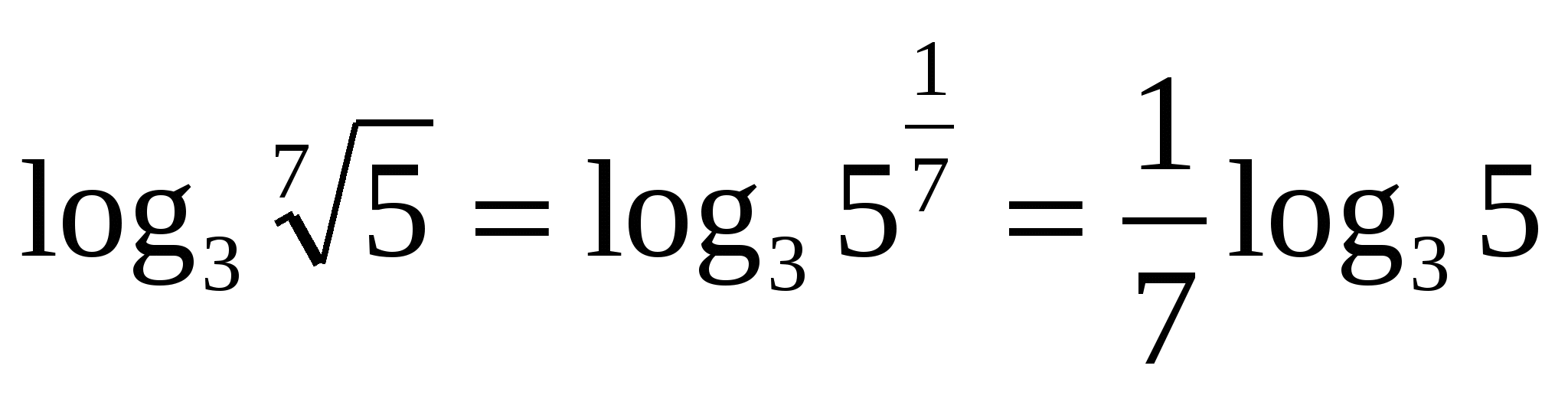
Z
1 užduotis. Apskaičiuokite, jei

Supaprastinkime išraišką

Formulė

paskambino perėjimo prie naujo pagrindo formulė.

Z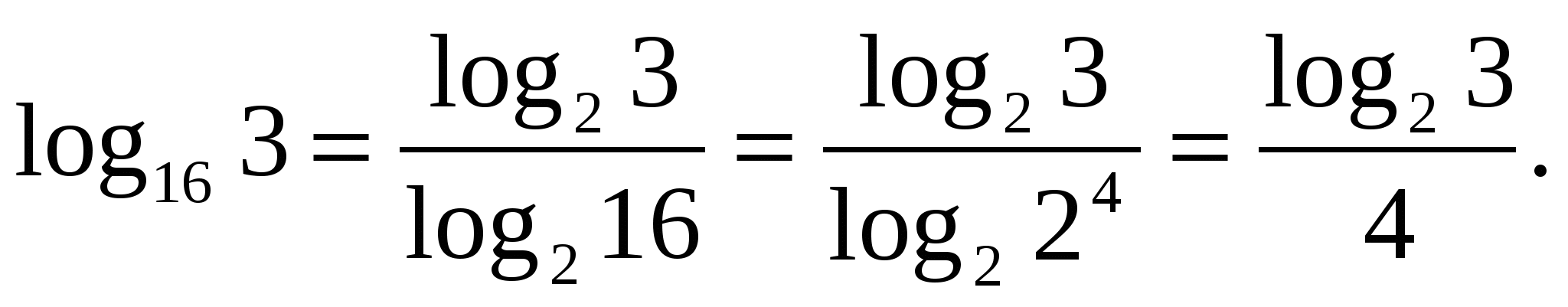

1 užduotis. Išreikškite 2 bazės logaritmu.

2 užduotis. Apskaičiuokite

TsOR 5

TsOR 6

Pavyzdžiui,

Z

1 užduotis. Apskaičiuokite

Z
2 užduotis. Apskaičiuokite

9) Logaritmines transformacijas galima pradėti tik tais atvejais, kai jei prisiminsite visas logaritmų savybes. Jas pakartoję, apsvarstysime logaritminių išraiškų transformavimo užduotis iš kitos pusės.

Norint konvertuoti logaritminių išraiškų sumą arba skirtumą, kartais pakanka naudoti logaritmo apibrėžimą, o dažniausiai sandaugos ar koeficiento logaritmo savybes.

Z
1 užduotis. Apskaičiuokite

Išspręskime tai dviem būdais.

1 būdas, naudojant logaritmo apibrėžimą:

2 metodas, pagrįstas koeficiento logaritmo savybė:

2 užduotis. Raskite posakio prasmę

Pirmiausia pritaikykime formulę sandaugos logaritmas, tada logaritmo apibrėžimas.

Pagrindinė logaritminė tapatybė naudojama konvertuojant išraiškas, kuriose logaritmas yra eksponentas. Tokių operacijų idėja yra gauti vienodas logaritmo galių ir bazių bazes.

Kartais reikia transformuoti išraišką pagal logaritmo savybes ir laipsnio savybes naudodamiesi perėjimo formule galite lengvai pereiti iš vienos bazės į kitą. Kitais atvejais turėtų būti taikomos kelios savybės.

Z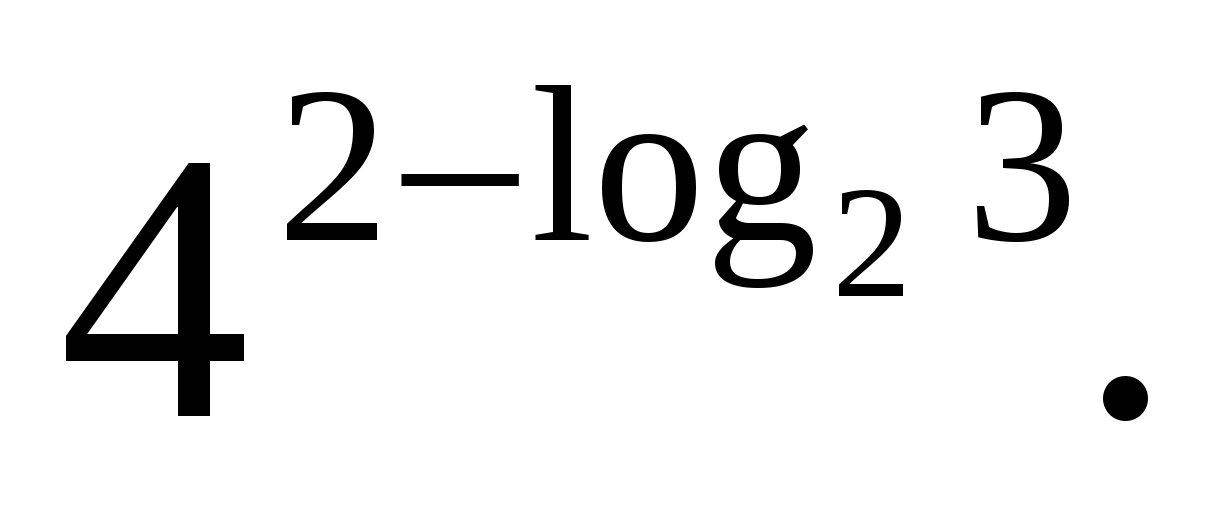
3 užduotis. Apskaičiuokite

Z
4 užduotis. Raskite posakio prasmę

5 užduotis. Raskite posakio prasmę

Z
6 užduotis. Išreikškite jį kaip logaritmų skirtumą

N
Didžiausias sunkumas yra logaritmines išraiškas konvertuoti į radikalą. Transformacijų procese būtina atsižvelgti į logaritminių reiškinių modulius, kurių atskleidimui reikia palyginti iracionaliuosius skaičius arba racionaliuosius ir neracionalus skaičius. Veiksime nuosekliai. Pažvelkime į išraišką po vidiniu radikalu.

Pakeiskime jį originalia išraiška.

Pažymėtina, kad su logaritminių išraiškų transformacija galima susidurti ir sprendžiant lygtis bei nelygybes ar tiriant funkcijas, todėl jos gali būti implicitiniu pavidalu B ir C grupių užduotyse.

10) Apibendrinant klausimus.

Vadinamas logaritmas iki 10 bazės

pagrindinis logaritmas

pagrindinis logaritmas

natūralusis logaritmas

dešimtainis logaritmas

2) Kokių vertybių tai gali turėti?x išraiškoje

Vertė neapibrėžta

5) Pateikite santykį, kuris tinka visiemsx ≠ 0 .

6) Nurodykite teisingą perėjimo į naują bazę formulės santykį.

7) Nurodykite teisingą lygybę

11) Kontrolinis bandymas.

Logaritmus, kaip ir bet kokius skaičius, galima visais būdais sudėti, atimti ir transformuoti. Bet kadangi logaritmai nėra visiškai įprasti skaičiai, čia yra taisyklės, kurios vadinamos pagrindinės savybės.

Jūs tikrai turite žinoti šias taisykles – be jų nepavyks išspręsti nė vienos rimtos logaritminės problemos. Be to, jų labai mažai – viską gali išmokti per vieną dieną. Taigi pradėkime.

Logaritmų pridėjimas ir atėmimas

Apsvarstykite du logaritmus su tais pačiais pagrindais: log a x ir žurnalas a y. Tada juos galima pridėti ir atimti, ir:

1. žurnalas a x+ žurnalas a y= žurnalas a (x · y);
2. žurnalas a x− žurnalas a y= žurnalas a (x : y).

Taigi logaritmų suma lygi sandaugos logaritmui, o skirtumas lygus koeficiento logaritmui. Atkreipkite dėmesį: pagrindinis dalykas čia yra identiškais pagrindais. Jei priežastys skiriasi, šios taisyklės neveikia!

Šios formulės padės apskaičiuoti logaritminę išraišką net tada, kai neatsižvelgiama į atskiras jos dalis (žr. pamoką „Kas yra logaritmas“). Pažvelkite į pavyzdžius ir pamatykite:

Rąstas 6 4 + rąstas 6 9.

Kadangi logaritmai turi tas pačias bazes, naudojame sumos formulę:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Užduotis. Raskite išraiškos reikšmę: log 2 48 − log 2 3.

Pagrindai yra vienodi, mes naudojame skirtumo formulę:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Užduotis. Raskite išraiškos reikšmę: log 3 135 − log 3 5.

Vėlgi, bazės yra tos pačios, todėl turime:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kaip matote, pradinės išraiškos yra sudarytos iš „blogų“ logaritmų, kurie nėra skaičiuojami atskirai. Bet po transformacijų gaunami visiškai normalūs skaičiai. Daugelis remiasi šiuo faktu bandymai. Taip, vieningo valstybinio egzamino metu į testus panašūs posakiai siūlomi labai rimtai (kartais praktiškai be pakeitimų).

Rodiklio išskyrimas iš logaritmo

Dabar šiek tiek apsunkinkime užduotį. Ką daryti, jei logaritmo pagrindas arba argumentas yra laipsnis? Tada šio laipsnio rodiklis gali būti paimtas iš logaritmo ženklo pagal šias taisykles:

Nesunku pastebėti, kad paskutinė taisyklė seka pirmąsias dvi. Bet vis tiek geriau tai atsiminti - kai kuriais atvejais tai žymiai sumažins skaičiavimų skaičių.

Žinoma, visos šios taisyklės turi prasmę, jei laikomasi logaritmo ODZ: a > 0, a ≠ 1, x> 0. Ir dar vienas dalykas: išmokite taikyti visas formules ne tik iš kairės į dešinę, bet ir atvirkščiai, t.y. Skaičius prieš logaritmo ženklą galite įvesti į patį logaritmą. Tai yra tai, ko dažniausiai reikia.

Užduotis. Raskite išraiškos reikšmę: log 7 49 6 .

Atsikratykime argumento laipsnio naudodami pirmąją formulę:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Užduotis. Raskite posakio prasmę:

[Paveikslo antraštė]

Atkreipkite dėmesį, kad vardiklyje yra logaritmas, kurio pagrindas ir argumentas yra tikslieji laipsniai: 16 = 2 4 ; 49 = 7 2. Turime:

[Paveikslo antraštė]

Manau, kad paskutinis pavyzdys reikalauja šiek tiek paaiškinimo. Kur dingo logaritmai? Iki pat paskutinė akimirka dirbame tik su vardikliu. Pateikėme ten stovinčio logaritmo bazę ir argumentą galių pavidalu ir išėmėme eksponentus - gavome „trijų aukštų“ trupmeną.

Dabar pažvelkime į pagrindinę dalį. Skaitiklyje ir vardiklyje yra tas pats skaičius: log 2 7. Kadangi log 2 7 ≠ 0, tai trupmeną galime sumažinti – vardiklyje liks 2/4. Pagal aritmetikos taisykles keturis galima perkelti į skaitiklį, kas ir buvo padaryta. Rezultatas buvo atsakymas: 2.

Perėjimas prie naujo pagrindo

Kalbėdamas apie logaritmų sudėjimo ir atėmimo taisykles, konkrečiai pabrėžiau, kad jos veikia tik su tais pačiais pagrindais. O jei priežastys kitokios? O jei jie nėra tikslūs to paties skaičiaus laipsniai?

Į pagalbą ateina perėjimo prie naujo pagrindo formulės. Suformuluokime juos teoremos forma:

Tegu pateikiamas logaritmo žurnalas a x. Tada už bet kokį skaičių c toks kad c> 0 ir c≠ 1, lygybė yra teisinga:

[Paveikslo antraštė]

Visų pirma, jei įdėtume c = x, gauname:

[Paveikslo antraštė]

Iš antrosios formulės išplaukia, kad logaritmo bazę ir argumentą galima sukeisti, tačiau tokiu atveju „apverčiama“ visa išraiška, t.y. vardiklyje atsiranda logaritmas.

Šios formulės retai randamos įprastose skaitinėse išraiškose. Įvertinti, kiek jie patogūs, galima tik apsisprendus logaritmines lygtis ir nelygybės.

Tačiau yra problemų, kurių niekaip nepavyks išspręsti, išskyrus persikėlimą į naują fondą. Pažvelkime į porą iš šių:

Užduotis. Raskite išraiškos reikšmę: log 5 16 log 2 25.

Atkreipkite dėmesį, kad abiejų logaritmų argumentuose yra tikslios galios. Išimkime rodiklius: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Dabar „atsukkime“ antrąjį logaritmą:

[Paveikslo antraštė]

Kadangi sandauga nesikeičia keičiant veiksnius, ramiai padauginome keturis ir du, o tada nagrinėjome logaritmus.

Užduotis. Raskite išraiškos reikšmę: log 9 100 lg 3.

Pirmojo logaritmo pagrindas ir argumentas yra tikslios galios. Užsirašykime tai ir atsikratykime rodiklių:

[Paveikslo antraštė]

Dabar atsikratykime dešimtainio logaritmo, pereidami prie naujos bazės:

[Paveikslo antraštė]

Pagrindinė logaritminė tapatybė

Dažnai sprendimo procese skaičių reikia pateikti kaip logaritmą tam tikram pagrindui. Šiuo atveju mums padės šios formulės:

Pirmuoju atveju skaičius n tampa argumentu stovinčio laipsnio rodikliu. Skaičius n gali būti visiškai bet kas, nes tai tik logaritmo reikšmė.

Antroji formulė iš tikrųjų yra perfrazuotas apibrėžimas. Taip ji vadinama: pagrindinė logaritminė tapatybė.

Tiesą sakant, kas atsitiks, jei numeris b pakelti iki tokios galios, kad skaičius bšiai galiai suteikia skaičių a? Teisingai: jūs gaunate tą patį numerį a. Dar kartą atidžiai perskaitykite šią pastraipą – daugeliui žmonių ji užstringa.

Kaip ir formulės, skirtos pereiti prie naujos bazės, pagrindinė logaritminė tapatybė kartais yra vienintelis galimas sprendimas.

Užduotis. Raskite posakio prasmę:

[Paveikslo antraštė]

Atkreipkite dėmesį, kad log 25 64 = log 5 8 – tiesiog paėmė kvadratą iš logaritmo pagrindo ir argumento. Atsižvelgdami į galių dauginimo su ta pačia baze taisykles, gauname:

[Paveikslo antraštė]

Jei kas nežino, tai buvo tikra užduotis iš unifikuoto valstybinio egzamino :)

Logaritminis vienetas ir logaritminis nulis

Baigdamas pateiksiu dvi tapatybes, kurias vargu ar galima pavadinti savybėmis – veikiau tai yra logaritmo apibrėžimo pasekmės. Jie nuolat atsiranda problemose ir, stebėtinai, kelia problemų net „pažengusiems“ studentams.

1. žurnalas a a= 1 yra logaritminis vienetas. Prisiminkite kartą ir visiems laikams: logaritmas bet kokiam pagrindui a nuo šio pagrindo yra lygus vienetui.
2. žurnalas a 1 = 0 yra logaritminis nulis. Bazė a gali būti bet koks, bet jei argumente yra vienas, logaritmas lygus nuliui! Nes a 0 = 1 yra tiesioginė apibrėžimo pasekmė.

Tai visos savybės. Būtinai praktikuokite juos pritaikydami praktiškai! Pamokos pradžioje atsisiųskite cheat lapą, atsispausdinkite ir išspręskite problemas.

Kaip žinote, dauginant išraiškas su laipsniais, jų rodikliai visada sumuojasi (a b *a c = a b+c). Šį matematinį dėsnį išvedė Archimedas, o vėliau, VIII amžiuje, matematikas Virasenas sukūrė sveikųjų rodiklių lentelę. Jie buvo tie, kurie tarnavo tolesnis atidarymas logaritmus. Šios funkcijos naudojimo pavyzdžių galima rasti beveik visur, kur reikia supaprastinti sudėtingą dauginimą paprastu sudėjimu. Jei skaitydami šį straipsnį skirsite 10 minučių, paaiškinsime, kas yra logaritmai ir kaip su jais dirbti. Paprasta ir prieinama kalba.

Apibrėžimas matematikoje

Logaritmas yra tokios formos išraiška: log a b=c, tai yra, bet kurio neneigiamo skaičiaus (ty bet kurio teigiamo) „b“ logaritmas iki jo bazės „a“ laikomas laipsniu „c“. “, iki kurio reikia pakelti bazę „a“, kad galiausiai gautume reikšmę „b“. Išanalizuokime logaritmą naudodami pavyzdžius, tarkime, kad yra išraiška log 2 8. Kaip rasti atsakymą? Tai labai paprasta, reikia rasti tokią galią, kad nuo 2 iki reikiamos galios gautumėte 8. Galvoje atlikę keletą skaičiavimų, gauname skaičių 3! Ir tai tiesa, nes 2 iki 3 laipsnio suteikia atsakymą kaip 8.

Logaritmų tipai

Daugeliui studentų ši tema atrodo sudėtinga ir nesuprantama, tačiau iš tikrųjų logaritmai nėra tokie baisūs, svarbiausia suprasti jų bendrą reikšmę ir prisiminti jų savybes bei kai kurias taisykles. Yra trys atskiros rūšys logaritminės išraiškos:

1. Natūralusis logaritmas ln a, kur bazė yra Eulerio skaičius (e = 2,7).
2. Dešimtainė a, kur bazė yra 10.
3. Bet kurio skaičiaus b logaritmas bazei a>1.

Kiekvienas iš jų yra išspręstas standartiniu būdu, įskaitant supaprastinimą, sumažinimą ir vėlesnį redukavimą iki vieno logaritmo naudojant logaritmines teoremas. Norėdami gauti teisingas logaritmų reikšmes, spręsdami turėtumėte atsiminti jų savybes ir veiksmų seką.

Taisyklės ir kai kurie apribojimai

Matematikoje yra keletas taisyklių-apribojimų, kurie priimami kaip aksioma, tai yra, jie nėra diskutuojami ir yra tiesa. Pavyzdžiui, neįmanoma skaičių padalyti iš nulio, taip pat neįmanoma išgauti neigiamų skaičių lyginės šaknies. Logaritmai taip pat turi savo taisykles, kurių laikydamiesi galite lengvai išmokti dirbti net su ilgomis ir talpiomis logaritminėmis išraiškomis:

• Bazė „a“ visada turi būti didesnė už nulį, o ne lygi 1, kitaip išraiška praras savo prasmę, nes „1“ ir „0“ bet kokiu laipsniu visada yra lygūs jų reikšmėms;
• jei a > 0, tai a b >0, pasirodo, kad „c“ taip pat turi būti didesnis už nulį.

Kaip išspręsti logaritmus?

Pavyzdžiui, pateikiama užduotis rasti atsakymą į lygtį 10 x = 100. Tai labai paprasta, reikia pasirinkti laipsnį, padidinant skaičių dešimt, iki kurio gauname 100. Tai, žinoma, yra 10 2 = 100.

Dabar pavaizduokime šią išraišką logaritmine forma. Gauname logaritmą 10 100 = 2. Sprendžiant logaritmus visi veiksmai praktiškai susilieja, kad rastų laipsnį, į kurį reikia įvesti logaritmo bazę, norint gauti duotą skaičių.

Norėdami tiksliai nustatyti nežinomo laipsnio reikšmę, turite išmokti dirbti su laipsnių lentele. Tai atrodo taip:

Kaip matote, kai kuriuos eksponentus galima atspėti intuityviai, jei turite techninį protą ir išmanote daugybos lentelę. Tačiau didesnėms vertėms jums reikės maitinimo stalo. Jį gali naudoti net tie, kurie nieko nežino apie kompleksą matematines temas. Kairiajame stulpelyje yra skaičiai (a bazė), viršutinė eilutė skaičiai yra laipsnio c reikšmė, iki kurios pakeliamas skaičius a. Sankryžoje langeliuose yra skaičių reikšmės, kurios yra atsakymas (a c = b). Paimkime, pavyzdžiui, patį pirmąjį langelį su skaičiumi 10 ir padėkite jį kvadratu, gausime reikšmę 100, kuri yra nurodyta mūsų dviejų langelių sankirtoje. Viskas taip paprasta ir lengva, kad supras net pats tikriausias humanistas!

Lygtys ir nelygybės

Pasirodo, tam tikromis sąlygomis eksponentas yra logaritmas. Todėl bet kurios matematinės skaitinės išraiškos gali būti užrašytos kaip logaritminė lygybė. Pavyzdžiui, 3 4 =81 gali būti parašytas kaip 81 bazinis 3 logaritmas, lygus keturiems (log 3 81 = 4). Už neigiamų galių taisyklės tos pačios: 2 -5 = 1/32 rašome kaip logaritmą, gauname log 2 (1/32) = -5. Viena įdomiausių matematikos skyrių yra „logaritmų“ tema. Žemiau pažvelgsime į lygčių pavyzdžius ir sprendimus, iš karto ištyrę jų savybes. Dabar pažiūrėkime, kaip atrodo nelygybės ir kaip jas atskirti nuo lygčių.

Duota tokios formos išraiška: log 2 (x-1) > 3 – tai yra logaritminė nelygybė, nes nežinoma reikšmė "x" yra po logaritmo ženklu. Taip pat išraiškoje lyginami du dydžiai: norimo skaičiaus logaritmas su baziniu du yra didesnis nei skaičius trys.

Svarbiausias skirtumas tarp logaritminių lygčių ir nelygybių yra tas, kad lygtys su logaritmais (pavyzdžiui, logaritmas 2 x = √9) reiškia vieną ar daugiau konkrečių skaitinių reikšmių atsakyme, o sprendžiant nelygybę, tiek priimtinų intervalų. reikšmės ir taškai nustatomi pažeidžiant šią funkciją. Todėl atsakymas yra ne paprastas atskirų skaičių rinkinys, kaip lygties atsakyme, o ištisinė skaičių seka arba rinkinys.

Pagrindinės teoremos apie logaritmus

Sprendžiant primityvias logaritmo reikšmių radimo užduotis, jo savybės gali būti nežinomos. Tačiau kalbant apie logaritmines lygtis ar nelygybes, pirmiausia reikia aiškiai suprasti ir praktiškai pritaikyti visas pagrindines logaritmų savybes. Vėliau pažvelgsime į lygčių pavyzdžius, pirmiausia pažvelkime į kiekvieną ypatybę išsamiau.

1. Pagrindinė tapatybė atrodo taip: a logaB =B. Jis taikomas tik tada, kai a yra didesnis nei 0, nelygus vienetui, o B yra didesnis už nulį.
2. Produkto logaritmą galima pavaizduoti tokia formule: log d (s 1 * s 2) = log d s 1 + log d s 2. Šiuo atveju būtina sąlyga yra: d, s1 ir s2 > 0; a≠1. Galite pateikti šios logaritminės formulės įrodymą su pavyzdžiais ir sprendimu. Tegu log a s 1 = f 1 ir log a s 2 = f 2, tada a f1 = s 1, a f2 = s 2. Gauname, kad s 1 * s 2 = a f1 *a f2 = a f1+f2 (ypatybės laipsniai ), o tada pagal apibrėžimą: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, ką reikėjo įrodyti.
3. Dalinio logaritmas atrodo taip: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Teorema formulės pavidalu įgauna tokią formą: log a q b n = n/q log a b.

Ši formulė vadinama „logaritmo laipsnio savybe“. Tai primena įprastų laipsnių savybes, ir tai nenuostabu, nes visa matematika remiasi natūraliais postulatais. Pažiūrėkime į įrodymą.

Tegu log a b = t, pasirodo a t =b. Jei abi dalis pakelsime laipsniu m: a tn = b n ;

bet kadangi a tn = (a q) nt/q = b n, todėl log a q b n = (n*t)/t, tada log a q b n = n/q log a b. Teorema įrodyta.

Problemų ir nelygybių pavyzdžiai

Dažniausiai pasitaikančios logaritmų problemos yra lygčių ir nelygybių pavyzdžiai. Jie yra beveik visose probleminėse knygose, taip pat yra privaloma matematikos egzaminų dalis. Dėl stojimo į universitetą arba išlaikymo stojamieji egzaminai matematikoje reikia mokėti teisingai išspręsti tokius uždavinius.

Deja, nėra vieno plano ar schemos, kaip išspręsti ir nustatyti nežinomą logaritmo reikšmę, tačiau jis gali būti pritaikytas kiekvienai matematinei nelygybei ar logaritminei lygčiai. tam tikras taisykles. Visų pirma, jūs turėtumėte išsiaiškinti, ar posakis gali būti supaprastintas ar sukelti bendra išvaizda. Galite supaprastinti ilgas logaritmines išraiškas, jei teisingai naudojate jų savybes. Greitai su jais susipažinkime.

Spręsdami logaritmines lygtis turime nustatyti, kokio tipo logaritmą turime: pavyzdinėje išraiškoje gali būti natūralusis logaritmas arba dešimtainis.

Štai pavyzdžiai ln100, ln1026. Jų sprendimas yra susijęs su tuo, kad jie turi nustatyti galią, kuriai bazė 10 bus lygi 100 ir 1026. Natūralių logaritmų sprendimams reikia taikyti logaritminės tapatybės arba jų savybes. Pažvelkime į sprendimą su pavyzdžiais logaritminės problemos skirtingų tipų.

Kaip naudoti logaritmo formules: su pavyzdžiais ir sprendimais

Taigi, pažvelkime į pagrindinių logaritmų teoremų naudojimo pavyzdžius.

1. Produkto logaritmo savybė gali būti naudojama atliekant užduotis, kur reikia plėsti puiki vertė skaičius b į paprastesnius veiksnius. Pavyzdžiui, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Atsakymas yra 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kaip matote, naudojant ketvirtąją logaritmo galios savybę, mums pavyko išspręsti iš pažiūros sudėtingą ir neišsprendžiamą išraišką. Jums tereikia apskaičiuoti bazę ir išimti eksponentų reikšmes iš logaritmo ženklo.

Vieningo valstybinio egzamino užduotys

Logaritmai dažnai aptinkami stojamuosiuose egzaminuose, ypač daug logaritminių uždavinių – vieningame valstybiniame egzamine (valstybinis egzaminas visiems abiturientams). Paprastai šios užduotys pateikiamos ne tik A dalyje (lengviausia egzamino dalis), bet ir C dalyje (sudėtingiausios ir didžiausios užduotys). Egzaminas reikalauja tikslių ir nepriekaištingų temos „Natūralūs logaritmai“ išmanymo.

Pavyzdžiai ir problemų sprendimai paimti iš oficialaus Vieningo valstybinio egzamino parinktys. Pažiūrėkime, kaip tokios užduotys sprendžiamos.

Duotas log 2 (2x-1) = 4. Sprendimas:
perrašykime išraišką, šiek tiek supaprastindami log 2 (2x-1) = 2 2, pagal logaritmo apibrėžimą gauname, kad 2x-1 = 2 4, todėl 2x = 17; x = 8,5.

• Geriausia visus logaritmus sumažinti iki vienodo pagrindo, kad sprendimas nebūtų sudėtingas ir painus.
• Visos išraiškos po logaritmo ženklu nurodomos kaip teigiamos, todėl, kai po logaritmo ženklu esančios išraiškos ir jo bazės eksponentas išimamas kaip daugiklis, po logaritmu likusi išraiška turi būti teigiama.