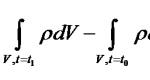Trigonométrique les fonctions périodique, c'est-à-dire qu'ils sont répétés après une certaine période. De ce fait, il suffit d’étudier la fonction sur cet intervalle et d’étendre les propriétés découvertes à toutes les autres périodes.

Instructions

1. Si on vous donne une expression primitive dans laquelle il n'y a qu'une seule fonction trigonométrique (sin, cos, tg, ctg, sec, cosec), et que l'angle à l'intérieur de la fonction n'est multiplié par aucun nombre, et qu'il n'est lui-même élevé à aucun pouvoir - utilisez la définition. Pour les expressions contenant sin, cos, sec, cosec, n'hésitez pas à définir la période sur 2P, et si l'équation contient tg, ctg, alors P. Disons que pour la fonction y=2 sinx+5, la période sera égale à 2P .

2. Si l'angle x sous le signe d'une fonction trigonométrique est multiplié par un nombre, alors pour trouver la période de cette fonction, divisez la période typique par ce nombre. Disons que l'on vous donne une fonction y = sin 5x. La période typique d'un sinus est 2P ; en la divisant par 5, vous obtenez 2P/5 - c'est la période souhaitée de cette expression.

3. Pour trouver la période d’une fonction trigonométrique élevée à une puissance, évaluez la parité de la puissance. Pour un niveau égal, réduisez la période habituelle de moitié. Disons que si on vous donne la fonction y = 3 cos^2x, alors la période typique 2P diminuera de 2 fois, donc la période sera égale à P. Veuillez noter que les fonctions tg, ctg sont périodiques de P à chaque degré.

4. Si l'on vous donne une équation contenant le produit ou le quotient de deux fonctions trigonométriques, trouvez d'abord la période pour chacune d'elles séparément. Après cela, trouvez le nombre minimum qui contiendrait l’entier des deux périodes. Disons que la fonction y=tgx*cos5x est donnée. Pour la tangente, la période est P, pour le cosinus 5x, la période est 2P/5. Le nombre minimum dans lequel ces deux périodes peuvent être hébergées est de 2P, donc la période souhaitée est de 2P.

5. Si vous avez du mal à le faire de la manière suggérée ou si vous doutez du résultat, essayez de le faire par définition. Prenons T comme période de la fonction ; elle est supérieure à zéro. Remplacez l'expression (x + T) au lieu de x dans l'équation et résolvez l'égalité résultante comme si T était un paramètre ou un nombre. Ainsi, vous découvrirez la valeur de la fonction trigonométrique et pourrez trouver la plus petite période. Disons qu'à la suite du soulagement, vous obtenez le péché d'identité (T/2) = 0. La valeur minimale de T à laquelle elle est effectuée est 2P, ce sera le résultat de la tâche.

Une fonction périodique est une fonction qui répète ses valeurs après une période non nulle. Le point d'une fonction est un nombre qui, lorsqu'il est ajouté à l'argument d'une fonction, ne modifie pas la valeur de la fonction.

Tu auras besoin de

• Connaissance des mathématiques élémentaires et révision de base.

Instructions

1. Notons la période de la fonction f(x) par le nombre K. Notre tâche est de découvrir cette valeur de K. Pour ce faire, imaginons que la fonction f(x), en utilisant la définition d'une fonction périodique, on assimile f(x+K)=f(x).

2. Nous résolvons l’équation résultante concernant l’inconnue K, comme si x était une constante. Selon la valeur de K, il y aura plusieurs options.

3. Si K>0 – alors c'est la période de votre fonction. Si K=0 – alors la fonction f(x) n'est pas périodique. Si la solution de l'équation f(x+K)=f(x) n'existe pas pour tout K différent de zéro, alors une telle fonction est appelée apériodique et elle n'a pas non plus de période.

Vidéo sur le sujet

Note!
Toutes les fonctions trigonométriques sont périodiques et toutes les fonctions polynomiales de degré supérieur à 2 sont apériodiques.

Conseil utile
La période d'une fonction composée de 2 fonctions périodiques est le plus petit multiple universel des périodes de ces fonctions.

Les équations trigonométriques sont des équations qui contiennent des fonctions trigonométriques d'un argument inconnu (par exemple : 5sinx-3cosx =7). Afin d'apprendre à les résoudre, vous devez connaître quelques moyens de procéder.

Instructions

1. La résolution de telles équations comprend 2 étapes : la première consiste à reformer l’équation pour acquérir sa forme la plus simple. Les équations trigonométriques les plus simples sont : Sinx=a ; Cosx=a, etc.

2. La seconde est la solution de l'équation trigonométrique la plus simple obtenue. Il existe des méthodes de base pour résoudre des équations de ce type : Résolution algébrique. Cette méthode est connue à l’école, dans un cours d’algèbre. Autrement appelé la méthode de remplacement et de substitution de variables. À l'aide de formules de réduction, nous transformons, effectuons une substitution, puis trouvons les racines.

3. Factoriser une équation. Tout d’abord, nous déplaçons tous les termes vers la gauche et les factorisons.

4. Réduire l’équation à une équation homogène. Les équations sont dites homogènes si tous les termes sont du même degré et le sinus et le cosinus du même angle. Pour la résoudre, vous devez : d'abord transférer tous ses termes du côté droit vers le côté gauche ; retirer tous les facteurs universels des parenthèses ; assimiler les facteurs et les parenthèses à zéro ; les parenthèses égales donnent une équation homogène d'un degré inférieur, qui doit être divisée par cos (ou sin) au degré le plus élevé ; résoudre l’équation algébrique résultante concernant le bronzage.

5. La méthode suivante consiste à passer à un demi-angle. Disons, résolvez l'équation : 3 sin x – 5 cos x = 7. Passons au demi-angle : 6 sin (x / 2) · cos (x / 2) – 5 cos ? (x/2) + 5 péché ? (x / 2) = 7 péché ? (x/2) + 7 cos ? (x/ 2) , après quoi nous réduisons tous les termes en une seule partie (de préférence le côté droit) et résolvons l'équation.

6. Saisie de l'angle auxiliaire. Lorsque nous remplaçons la valeur entière cos(a) ou sin(a). Le signe « a » est un angle auxiliaire.

7. Une méthode pour reformer un produit en une somme. Ici, vous devez appliquer les formules appropriées. Disons étant donné : 2 sin x · sin 3x = cos 4x. Résolvez-le en transformant le côté gauche en une somme, soit : cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p/16 + pk/8.

8. La dernière méthode est appelée substitution multifonction. Nous transformons l'expression et apportons un changement, disons Cos(x/2)=u, puis résolvons l'équation avec le paramètre u. Lors de l'achat du total, nous convertissons la valeur en l'inverse.

Vidéo sur le sujet

Si l'on considère des points sur un cercle, alors les points x, x + 2π, x + 4π, etc. coïncident les uns avec les autres. Ainsi, trigonométrique les fonctions en ligne droite périodiquement répéter leur sens. Si la période est célèbre les fonctions, il est possible de construire une fonction sur cette période et de la répéter sur d'autres.

Instructions

1. La période est un nombre T tel que f(x) = f(x+T). Afin de trouver la période, résolvez l’équation correspondante en substituant x et x+T comme argument. Dans ce cas, ils utilisent les périodes déjà connues pour les fonctions. Pour les fonctions sinus et cosinus, la période est 2π, et pour les fonctions tangente et cotangente, elle est π.

2. Soit la fonction f(x) = sin^2(10x). Considérons l'expression sin^2(10x) = sin^2(10(x+T)). Utilisez la formule pour réduire le degré : sin^2(x) = (1 – cos 2x)/2. Ensuite, vous obtenez 1 – cos 20x = 1 – cos 20(x+T) ou cos 20x = cos (20x+20T). Sachant que la période du cosinus est 2π, 20T = 2π. Cela signifie T = π/10. T est la période minimale correcte, et la fonction sera répétée après 2T, et après 3T, et dans l'autre sens le long de l'axe : -T, -2T, etc.

Conseil utile
Utiliser des formules pour réduire le degré d'une fonction. Si vous connaissez déjà les périodes de certaines fonctions, essayez de réduire la fonction existante à celles connues.

L'examen d'une fonction pour déterminer sa régularité et son impair aide à construire un graphique de la fonction et à comprendre la nature de son comportement. Pour cette recherche, vous devez comparer cette fonction écrite pour l'argument « x » et pour l'argument « -x ».

Instructions

1. Notez la fonction que vous souhaitez étudier sous la forme y=y(x).

2. Remplacez l'argument de la fonction par « -x ». Remplacez cet argument par une expression fonctionnelle.

3. Simplifiez l'expression.

4. Ainsi, vous avez la même fonction écrite pour les arguments « x » et « -x ». Regardez ces deux entrées. Si y(-x)=y(x), alors c'est une fonction paire. Si y(-x)=-y(x), alors c'est une fonction impaire. S'il est impossible de disons à propos d'une fonction que y (-x)=y(x) ou y(-x)=-y(x), alors par la propriété de parité c'est une fonction de forme universelle. Autrement dit, ce n'est ni pair ni impair.

5. Notez vos découvertes. Vous pouvez désormais les utiliser pour construire un graphique d'une fonction ou dans une future étude analytique des propriétés d'une fonction.

6. Il est également possible de parler de régularité et d'impair d'une fonction dans le cas où le graphique de la fonction est déjà donné. Disons que le graphique est le résultat d'une expérience physique. Si le graphique d'une fonction est symétrique par rapport à l'axe des ordonnées, alors y(x) est une fonction paire. Si le graphique d'une fonction est symétrique par rapport à l'axe des abscisses, alors x(y) est une fonction paire. x(y) est une fonction inverse de la fonction y(x). Si le graphique d'une fonction est symétrique par rapport à l'origine (0,0), alors y(x) est une fonction impaire. La fonction inverse x(y) sera également impaire.

7. Il est important de se rappeler que l'idée de régularité et d'impair d'une fonction a un lien direct avec le domaine de définition de la fonction. Si, disons, une fonction paire ou impaire n’existe pas à x=5, alors elle n’existe pas à x=-5, ce qui ne peut pas être dit d’une fonction de forme universelle. Lors de l'établissement des parités paires et impaires, faites attention au domaine de la fonction.

8. La recherche d'une fonction pour la régularité et l'impair est en corrélation avec la recherche d'un ensemble de valeurs de fonction. Pour retrouver l'ensemble des valeurs d'une fonction paire, il suffit de regarder la moitié de la fonction, à droite ou à gauche de zéro. Si à x>0 la fonction paire y(x) prend les valeurs de A à B, alors elle prendra les mêmes valeurs à x<0.Для нахождения множества значений, принимаемых нечетной функцией, тоже довольно разглядеть только одну часть функции. Если при x>0 fonction impaire y(x) prend une plage de valeurs de A à B, puis à x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).

« Trigonométrique » a autrefois commencé à être appelé fonctions qui sont déterminées par la dépendance des angles aigus d'un triangle rectangle sur la longueur de ses côtés. De telles fonctions comprennent, d'une part, le sinus et le cosinus, et d'autre part, l'inverse de ces fonctions, sécante et cosécante, leurs dérivées tangente et cotangente, ainsi que les fonctions inverses arcsinus, arccosinus, etc. Il est plus positif de ne pas parler de la « solution » de telles fonctions, mais sur leur « calcul », c'est-à-dire sur la recherche d'une valeur numérique.

Instructions

1. Si l'argument de la fonction trigonométrique est inconnu, alors sa valeur peut être calculée par une méthode indirecte basée sur les définitions de ces fonctions. Pour ce faire, vous devez connaître les longueurs des côtés du triangle, dont il faut calculer la fonction trigonométrique pour l'un des angles. Disons, par définition, que le sinus d'un angle aigu dans un triangle rectangle est le rapport de la longueur de la jambe opposée à cet angle à la longueur de l'hypoténuse. Il s'ensuit que pour trouver le sinus d'un angle il suffit de connaître les longueurs de ces 2 côtés. Une définition similaire stipule que le sinus d'un angle aigu est le rapport entre la longueur de la jambe adjacente à cet angle et la longueur de l'hypoténuse. La tangente d'un angle aigu peut être calculée en divisant la longueur de la branche opposée par la longueur de la branche adjacente, et la cotangente nécessite de diviser la longueur de la branche adjacente par la longueur de la branche opposée. Pour calculer la sécante d'un angle aigu, vous devez trouver le rapport entre la longueur de l'hypoténuse et la longueur de la jambe adjacente à l'angle requis, et la cosécante est déterminée par le rapport de la longueur de l'hypoténuse à la longueur de la jambe opposée.

2. Si l'argument de la fonction trigonométrique est correct, vous n'avez pas besoin de connaître les longueurs des côtés du triangle - vous pouvez utiliser des tableaux de valeurs ou des calculatrices de fonctions trigonométriques. Une telle calculatrice est incluse dans les programmes standards du système d'exploitation Windows. Pour le lancer, vous pouvez appuyer sur la combinaison de touches Win + R, entrer la commande calc et cliquer sur le bouton « OK ». Dans l'interface du programme, vous devez développer la section « Affichage » et sélectionner l'élément « Ingénieur » ou « Scientifique ». Après cela, il est possible d’introduire l’argument de la fonction trigonométrique. Pour calculer les fonctions sinus, cosinus et tangente, après avoir saisi la valeur, cliquez sur le bouton d'interface correspondant (sin, cos, tg), et pour trouver leur arc sinus inverse, arc cosinus et arc tangente, vous devez cocher au préalable la case Inv.

3. Il existe également des méthodes alternatives. L'une d'elles consiste à accéder au site Web du moteur de recherche Nigma ou Google et à saisir la fonction souhaitée et son argument sous forme de requête de recherche (par exemple, sin 0,47). Ces moteurs de recherche disposent de calculatrices intégrées. Ainsi, après avoir envoyé une telle demande, vous recevrez la valeur de la fonction trigonométrique que vous avez saisie.

Vidéo sur le sujet

Astuce 7 : Comment découvrir la valeur des fonctions trigonométriques

Les fonctions trigonométriques sont apparues pour la première fois comme outils de calculs mathématiques abstraits des dépendances des valeurs des angles aigus dans un triangle rectangle sur les longueurs de ses côtés. Aujourd'hui, ils sont largement utilisés dans les domaines scientifiques et techniques de l'activité humaine. Pour les calculs utilitaires de fonctions trigonométriques à partir d'arguments donnés, vous pouvez utiliser divers outils - plusieurs d'entre eux particulièrement accessibles sont décrits ci-dessous.

Instructions

1. Utilisez, par exemple, le programme de calculatrice installé par défaut avec le système d'exploitation. Il s'ouvre en sélectionnant l'élément « Calculatrice » dans le dossier « Service » de la sous-section « Typique », située dans la section « Tous les programmes ». Cette section peut être trouvée en ouvrant le menu principal du système d'exploitation en cliquant sur le bouton « Démarrer ». Si vous utilisez la version Windows 7, vous saisirez probablement simplement le mot « Calculatrice » dans le champ « Découvrir les programmes et fichiers » du menu principal, puis cliquerez sur le lien correspondant dans les résultats de recherche.

2. Saisissez la valeur de l'angle pour lequel vous souhaitez calculer la fonction trigonométrique, puis cliquez sur le bouton correspondant à cette fonction - sin, cos ou tan. Si vous êtes préoccupé par les fonctions trigonométriques inverses (arc sinus, arc cosinus ou arc tangente), cliquez d'abord sur le bouton intitulé Inv - il inverse les fonctions attribuées aux boutons de guidage de la calculatrice.

3. Dans les versions antérieures du système d'exploitation (par exemple, Windows XP), pour accéder aux fonctions trigonométriques, vous devez ouvrir la section « Affichage » dans le menu de la calculatrice et sélectionner la ligne « Ingénierie ». De plus, au lieu du bouton Inv, l'interface des anciennes versions du programme comporte une case à cocher avec la même inscription.

4. Vous pouvez vous passer de calculatrice si vous avez accès à Internet. Il existe de nombreux services sur Internet proposant des calculatrices de fonctions trigonométriques organisées de différentes manières. L'une des options particulièrement pratiques est intégrée au moteur de recherche Nigma. En accédant à sa page principale, entrez simplement la valeur qui vous inquiète dans le champ de requête de recherche - par exemple « arc tangent 30 degrés ». Après avoir cliqué sur le bouton « Détecter ! » Le moteur de recherche calculera et affichera le résultat du calcul - 0,482347907101025.

Vidéo sur le sujet

La trigonométrie est une branche des mathématiques permettant de comprendre les fonctions qui expriment différentes dépendances des côtés d'un triangle rectangle sur les valeurs des angles aigus au niveau de l'hypoténuse. De telles fonctions étaient appelées trigonométriques et pour faciliter leur utilisation, des fonctions trigonométriques ont été dérivées identités .

Performance identités en mathématiques, cela désigne une égalité qui est satisfaite pour toutes les valeurs des arguments des fonctions qui y sont incluses. Trigonométrique identités sont des égalités de fonctions trigonométriques, confirmées et acceptées pour simplifier le travail avec des formules trigonométriques.Une fonction trigonométrique est une fonction élémentaire de la dépendance de l'une des branches d'un triangle rectangle sur la valeur de l'angle aigu à l'hypoténuse. Les six fonctions trigonométriques de base les plus souvent utilisées sont sin (sinus), cos (cosinus), tg (tangente), ctg (cotangente), sec (sécante) et cosec (cosécante). Ces fonctions sont appelées fonctions directes, il existe également des fonctions inverses, par exemple sinus - arc sinus, cosinus - arc cosinus, etc. Initialement, les fonctions trigonométriques se reflétaient dans la géométrie, après quoi elles se sont propagées à d'autres domaines scientifiques : physique, chimie, géographie, l'optique, la théorie des probabilités, ainsi que l'acoustique, la théorie musicale, la phonétique, l'infographie et bien d'autres. De nos jours, il est difficile d'imaginer des calculs mathématiques sans ces fonctions, même si dans un passé lointain elles n'étaient utilisées qu'en astronomie et en architecture. identités sont utilisés pour simplifier le travail avec de longues formules trigonométriques et les réduire à une forme digestible. Il existe six identités trigonométriques principales ; elles sont liées aux fonctions trigonométriques directes : tg ? = péché ?/cos ?; péché^2 ? + parce que ^2 ? = 1 ; 1 + tg^2 ? = 1/cos^2 ?; 1 + 1/tg^2 ? = 1/péché^2 ?; péché (?/2 – ?) = cos ?; cos (?/2 – ?) = sin ?. Ces identités facile à confirmer à partir des propriétés du rapport des côtés et des angles dans un triangle rectangle : sin ? = BC/AC = b/c; parce que ? = AB/AC = climatisation ; tg ? = b/a. La première identité tg ? = péché ?/cos ? découle du rapport des côtés du triangle et de l'exclusion du côté c (hypoténuse) lors de la division du péché par cos. L'identité ctg ? est définie de la même manière. = cos ?/sin ?, car ctg ? = 1/tg ?.Par le théorème de Pythagore a^2 + b^2 = c^2. Divisons cette égalité par c^2, nous obtenons la deuxième identité : a^2/c^2 + b^2/c^2 = 1 => sin^2 ? + cos^2 ? = 1.Troisième et quatrième identités obtenu en divisant respectivement par b^2 et a^2 : a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/péché^ ? ou 1 + ctg^2 ? = 1/sin^2 ?. Cinquième et sixième de base identités sont prouvés en déterminant la somme des angles aigus d'un triangle rectangle, qui est égale à 90° ou ?/2. Trigonométrique plus difficile identités: formules pour ajouter des arguments, des angles doubles et triples, réduire des degrés, reformer la somme ou le produit de fonctions, ainsi que des formules de substitution trigonométrique, à savoir expressions de fonctions trigonométriques de base par tg d'un demi-angle : sin ?= (2*tg ?/2)/(1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).

La nécessité de trouver le minimum signification mathématique les fonctions est d’un réel intérêt pour résoudre des problèmes appliqués, par exemple en économie. Énorme signification minimiser les pertes est essentiel pour les activités commerciales.

Instructions

1. Afin de découvrir le minimum signification les fonctions, il faut déterminer à quelle valeur de l’argument x0 l’inégalité y(x0) sera satisfaite ? y(x), où x ? x0. Comme d'habitude, ce problème est résolu sur un certain intervalle ou dans chaque plage de valeurs les fonctions, si aucun n'est spécifié. Un aspect de la solution consiste à trouver des points fixes.

2. Un point stationnaire s’appelle signification argument dans lequel la dérivée les fonctions va à zéro. D'après le théorème de Fermat, si une fonction différentiable prend une direction extrême significationà un moment donné (dans ce cas, un minimum local), alors ce point est stationnaire.

3. Le minimum signification la fonction prend souvent exactement ce point, mais elle ne peut pas être déterminée invariablement. De plus, il n’est pas toujours possible de dire avec précision quel est le minimum les fonctions ou il accepte l'infiniment petit signification. Puis, comme d'habitude, ils trouvent la limite vers laquelle elle tend à mesure qu'elle diminue.

4. Afin de déterminer le minimum signification les fonctions, vous devez effectuer une séquence d'actions composée de quatre étapes : trouver le domaine de définition les fonctions, acquisition de points fixes, aperçu des valeurs les fonctions en ces points et aux extrémités de l'intervalle, détecter le minimum.

5. Il s'avère qu'une fonction y(x) est donnée sur un intervalle avec des limites aux points A et B. Trouvez le domaine de sa définition et découvrez si l'intervalle est son sous-ensemble.

6. Calculer la dérivée les fonctions. Égalisez l’expression résultante à zéro et trouvez les racines de l’équation. Vérifiez si ces points stationnaires se situent dans l'espace. Dans le cas contraire, ils ne seront pas pris en compte ultérieurement.

7. Examinez l'écart pour le type de frontières : ouvertes, fermées, composées ou incommensurables. Ceci détermine la façon dont vous recherchez le minimum signification. Disons que le segment [A, B] est un intervalle fermé. Branchez-les dans la fonction et calculez les valeurs. Faites de même avec un point fixe. Sélectionnez le total le plus bas.

8. Avec des intervalles ouverts et incommensurables, la situation est un peu plus difficile. Ici, vous devrez rechercher des limites unilatérales qui ne donnent pas invariablement un résultat sans ambiguïté. Disons que pour un intervalle avec une frontière fermée et une frontière perforée [A, B), on devrait trouver une fonction en x = A et une limite unilatérale lim y en x ? B-0.

satisfaire le système d’inégalités :

b) Considérons un ensemble de nombres sur la droite numérique qui satisfont au système d'inégalités :

Trouvez la somme des longueurs des segments qui composent cet ensemble.

§ 7. Les formules les plus simples

Au § 3 nous avons établi la formule suivante pour les angles aigus α :

			sin2 α + cos2 α = 1.
				Même formule			quand,
				quand α est quelconque			en fait
				le, soit M un point en trigonométrie
				cercle ique correspondant à
				numéro α (Fig. 7.1). Alors		M a co-
				ordonnées x = cos α, y
				Cependant, tout point (x; y) situé sur
				cercle de rayon unité avec centre
				tromé à l'origine, satisfaisant
				satisfait l'équation x2 + y2		1, d'où
				cos2 α + sin2 α = 1, selon les besoins.

Ainsi, la formule cos2 α + sin2 α = 1 découle de l'équation du cercle. Il peut sembler que nous ayons ainsi donné une nouvelle preuve de cette formule pour les angles aigus (en comparaison avec celle indiquée au § 3, où nous avons utilisé le théorème de Pythagore). La différence, cependant, est purement externe : pour dériver l'équation d'un cercle x2 + y2 = 1, le même théorème de Pythagore est utilisé.

Pour les angles aigus nous avons également obtenu d'autres formules, par exemple

Selon le symbole, le côté droit est toujours non négatif, tandis que le côté gauche peut très bien être négatif. Pour que la formule soit vraie pour tout α, il faut qu’elle soit au carré. L’égalité résultante est : cos2 α = 1/(1 + tan2 α). Montrons que cette formule est vraie pour tout α:1

1/(1 + bronzage2			péché2 α			cos2α	Cos2α.
			cos2α			sin2α + cos2α

Problème 7.1. Dérivez toutes les formules ci-dessous à partir des définitions et de la formule sin2 α + cos2 α = 1 (nous en avons déjà prouvé certaines) :

sin2α + cos2α = 1 ;

tg2 α =

tg2α

sin2 α =

tg α · ctg α = 1 ;

cos2α

1 + tan2 α

ctg2 α

Ctg2

cos2α =

1 + lit2 α

péché2

Ces formules permettent, connaissant la valeur d'une des fonctions trigonométriques d'un nombre donné, de retrouver presque tout le reste.

nouveau Sachons, par exemple, que sin x = 1/2. Alors cos2 x =

1−sin2 x = 3/4, donc cos x est soit 3/2, soit − 3/2. Pour savoir lequel de ces deux nombres cos x est égal, des informations supplémentaires sont nécessaires.

Problème 7.2. Montrez avec des exemples que les deux cas ci-dessus sont possibles.

Problème 7.3. a) Soit tan x = −1. Trouvez le péché x. Combien de réponses ce problème a-t-il ?

b) Supposons, en plus des conditions du point a), que sin x< 0. Сколько теперь ответов у задачи?

1 Pour lequel tan α est défini, soit cos α 6= 0.

Problème 7.4. Soit sin x = 3/5, x [π/2; 3π/2]. Trouvez tgx.

Problème 7.5. Soit tan x = 3, cos x > sin x. Trouvez cos x, sin x.

Problème 7.6. Soit tg x = 3/5. Trouvez sin x + 2 cos x. cos x − 3 péché x

Problème 7.7. Prouvez les identités :

tan α − péché α

c) sin α + cos α cot α + sin α tan α + cos α =

Problème 7.8. Simplifiez les expressions :

a) (sin α + cos α)2 + (sin α − cos α)2 ; b) (tg α + ctg α)2 + (tg α − ctg α)2 ;

c) sin α(2 + cot α)(2 cot α + 1) − 5 cos α.

§ 8. Périodes de fonctions trigonométriques

Les nombres x, x+2π, x−2π correspondent au même point sur le cercle trigonométrique (si vous parcourez un cercle supplémentaire le long du cercle trigonométrique, vous reviendrez là où vous étiez). Cela implique les identités suivantes, qui ont déjà été discutées au § 5 :

sin(x + 2π) = sin(x − 2π) = sinx; cos(x + 2π) = cos(x − 2π) = cosx.

En relation avec ces identités, nous avons déjà utilisé le terme « période ». Donnons maintenant des définitions précises.

Définition. Le nombre T 6= 0 est appelé la période de la fonction f si pour tout x les égalités f(x − T) = f(x + T) = f(x) sont vraies (on suppose que x + T et x − T sont inclus dans le domaine de définition de la fonction , s'il inclut x). Une fonction est dite périodique si elle possède un point (au moins un).

Les fonctions périodiques apparaissent naturellement lors de la description de processus oscillatoires. L'un de ces processus a déjà été discuté au § 5. Voici d'autres exemples :

1) Soit ϕ = ϕ(t) l'angle de déviation du pendule oscillant de l'horloge par rapport à la verticale à l'instant t. Alors ϕ est une fonction périodique de t.

2) La tension (« différence de potentiel », comme dirait un physicien) entre deux prises d'une prise secteur, es-

qu'elle soit considérée en fonction du temps, est une fonction périodique1.

3) Écoutons le son musical. Alors la pression de l’air en un point donné est une fonction périodique du temps.

Si une fonction a une période T, alors les périodes de cette fonction seront également les nombres −T, 2T, −2T. . . - en un mot, tous les nombres nT, où n est un nombre entier différent de zéro. En effet, vérifions par exemple que f(x + 2T) = f(x) :

f(x + 2T) = f((x + T) + T) = f(x + T) = f(x).

Définition. La plus petite période positive d'une fonction f est - conformément au sens littéral des mots - un nombre positif T tel que T est une période de f et aucun nombre positif inférieur à T n'est une période de f.

Il n’est pas nécessaire qu’une fonction périodique ait la plus petite période positive (par exemple, une fonction constante a une période de n’importe quel nombre et, par conséquent, elle n’a pas la plus petite période positive). On peut aussi donner des exemples de fonctions périodiques non constantes qui n'ont pas la plus petite période positive. Néanmoins, dans les cas les plus intéressants, il existe la plus petite période positive des fonctions périodiques.

1 Lorsqu'ils disent « la tension dans le réseau est de 220 volts », ils entendent sa « valeur efficace », dont nous parlerons au § 21. La tension elle-même change tout le temps.

Riz. 8.1. Période de tangente et de cotangente.

En particulier, la plus petite période positive du sinus et du cosinus est 2π. Montrons cela, par exemple, pour la fonction y = sin x. Supposons que, contrairement à ce que nous prétendons, sinus ait une période T telle que 0< T < 2π. При x = π/2 имеем sin x = = 1. Будем теперь увеличивать x. В точке x + T значение синуса должно быть также равно 1. Но в следующий раз синус будет равен 1 только при x = (π/2) + 2π. Поэтому период синуса быть меньше 2π не может. Доказательство для косинуса аналогично.

La plus petite période positive de la fonction décrivant les oscillations (comme dans nos exemples 1 à 3) est simplement appelée période de ces oscillations.

Puisque 2π est la période du sinus et du cosinus, ce sera aussi la période de la tangente et de la cotangente. Cependant, pour ces fonctions, 2π n'est pas la plus petite période : la plus petite période positive de la tangente et de la cotangente sera π. En effet, les points correspondant aux nombres x et x + π sur le cercle trigonométrique sont diamétralement opposés : du point x au point x + 2π il faut parcourir une distance π exactement égale à la moitié du cercle. Maintenant, si nous utilisons la définition de la tangente et de la cotangente en utilisant les axes des tangentes et des cotangentes, les égalités tg(x + π) = tan x et ctg(x + π) = ctg x deviendront évidentes (Fig. 8.1). Il est facile de vérifier (nous proposerons de le faire dans les problèmes) que π est bien la plus petite période positive de la tangente et de la cotangente.

Une remarque sur la terminologie. Les mots « période d’une fonction » sont souvent utilisés pour signifier « la plus petite période positive ». Ainsi, si lors d'un examen on vous demande : « 100π est-il la période de la fonction sinusoïdale ? », ne vous précipitez pas pour répondre, mais précisez si vous parlez de la plus petite période positive ou d'une seule des périodes.

Les fonctions trigonométriques sont un exemple typique de fonctions périodiques : toute fonction périodique « pas très mauvaise » peut en quelque sorte être exprimée en termes de fonctions trigonométriques.

Problème 8.1. Trouver les plus petites périodes positives des fonctions :

				c) y = cos πx ;

d) y = cosx + cos(1,01x).

Problème 8.2. La dépendance de la tension dans un réseau à courant alternatif en fonction du temps est donnée par la formule U = U0 sin ωt (ici t est le temps, U est la tension, U0 et ω sont des constantes). La fréquence du courant alternatif est de 50 Hertz (cela signifie que la tension fait 50 oscillations par seconde).

a) Trouvez ω, en supposant que t est mesuré en secondes ;

b) Trouvez la période (la plus petite positive) de U en fonction de t.

Problème 8.3. a) Montrer que la plus petite période positive du cosinus est 2π ;

b) Montrer que la plus petite période positive de la tangente est égale à π.

Problème 8.4. Soit T la plus petite période positive de la fonction f. Montrer que toutes ses autres périodes sont de la forme nT pour certains entiers n.

Problème 8.5. Montrer que les fonctions suivantes ne sont pas périodiques.

>> Périodicité des fonctions y = sin x, y = cos x

§ 11. Périodicité des fonctions y = sin x, y = cos x

Dans les paragraphes précédents, nous avons utilisé sept propriétés les fonctions: domaine de définition, pair ou impair, monotonie, bornage, valeurs les plus grandes et les plus petites, continuité, plage de valeurs d'une fonction. Nous avons utilisé ces propriétés soit pour construire le graphe d'une fonction (cela s'est produit par exemple au § 9), soit pour lire le graphe construit (cela s'est produit par exemple au § 10). Le moment opportun est maintenant venu d’introduire une (huitième) propriété supplémentaire des fonctions, qui est clairement visible dans les constructions ci-dessus. graphiques fonctions y = sin x (voir Fig. 37), y = cos x (voir Fig. 41).

Définition. Une fonction est dite périodique s'il existe un nombre T non nul tel que pour tout x de l'ensemble, la double condition est vraie : égalité:

Le nombre T qui satisfait la condition spécifiée est appelé la période de la fonction y = f(x).
Il s'ensuit que, puisque pour tout x les égalités sont valables :

alors les fonctions y = sin x, y = cos x sont périodiques et le nombre est 2 P. sert de période pour les deux fonctions.
La périodicité d'une fonction est la huitième propriété promise des fonctions.

Regardez maintenant le graphique de la fonction y = sin x (Fig. 37). Pour construire une onde sinusoïdale, il suffit de tracer une de ses ondes (sur un segment puis de décaler cette onde le long de l'axe x de. En conséquence, en utilisant une onde, nous construirons le graphique entier.

Regardons du même point de vue le graphique de la fonction y = cos x (Fig. 41). On voit qu'ici, pour tracer un graphique, il suffit de tracer d'abord une onde (par exemple, sur le segment

Et puis déplacez-le le long de l'axe x en
En résumé, nous tirons la conclusion suivante.

Si la fonction y = f(x) a une période T, alors pour construire un graphique de la fonction, vous devez d'abord construire une branche (onde, partie) du graphique sur n'importe quel intervalle de longueur T (prendre le plus souvent un intervalle avec des extrémités en points puis décalez cette branche le long de l'axe des x vers la droite et la gauche vers T, 2T, ZT, etc.
Une fonction périodique a une infinité de périodes : si T est une période, alors 2T est une période, et ZT est une période, et -T est une période ; En général, une période est n'importe quel nombre de la forme KT, où k = ±1, ±2, ± 3... Habituellement, on essaie, si possible, d'isoler la plus petite période positive : on l'appelle la période principale.
Ainsi, tout nombre de la forme 2pk, où k = ±1, ± 2, ± 3, est la période des fonctions y = sinn x, y = cos x ; 2n est la période principale des deux fonctions.

Exemple. Retrouvez la période principale de la fonction :

UN) Soit T la période principale de la fonction y = sin x. Mettons

Pour que le nombre T soit une période d'une fonction, l'identité Mais, puisqu'il s'agit de trouver la période principale, on obtient
b) Soit T la période principale de la fonction y = cos 0,5x. Mettons f(x)=cos 0,5x. Alors f(x + T)=cos 0,5(x + T)=cos (0,5x + 0,5T).

Pour que le nombre T soit une période de la fonction, l'identité cos (0,5x + 0,5T) = cos 0,5x doit être vérifiée.

Cela signifie 0,5t = 2pp. Mais, puisqu'il s'agit de trouver la période principale, nous obtenons 0,5T = 2 l, T = 4 l.

La généralisation des résultats obtenus dans l'exemple est l'énoncé suivant : la période principale de la fonction

A.G. Mordkovich Algèbre 10e année

Contenu de la leçon notes de cours cadre de support présentation de cours méthodes d'accélération technologies interactives Pratique tâches et exercices ateliers d'autotest, formations, cas, quêtes devoirs questions de discussion questions rhétoriques des étudiants Illustrations audio, clips vidéo et multimédia photographies, images, graphiques, tableaux, diagrammes, humour, anecdotes, blagues, bandes dessinées, paraboles, dictons, mots croisés, citations Modules complémentaires résumés articles astuces pour les curieux crèches manuels scolaires dictionnaire de base et supplémentaire des termes autres Améliorer les manuels et les leçonscorriger les erreurs dans le manuel mise à jour d'un fragment dans un manuel, éléments d'innovation dans la leçon, remplacement des connaissances obsolètes par de nouvelles Uniquement pour les enseignants des leçons parfaites plan de calendrier pour l'année; recommandations méthodologiques; programmes de discussion Leçons intégrées

Argument x, alors il est appelé périodique s'il existe un nombre T tel que pour tout x F(x + T) = F(x). Ce nombre T est appelé la période de la fonction.

Il peut y avoir plusieurs périodes. Par exemple, la fonction F = const prend la même valeur pour n'importe quelle valeur de l'argument, et donc n'importe quel nombre peut être considéré comme sa période.

Habituellement, vous vous intéressez à la plus petite période non nulle d’une fonction. Par souci de concision, cela s’appelle simplement un point.

Un exemple classique de fonctions périodiques est trigonométrique : sinus, cosinus et tangente. Leur période est la même et égale à 2π, c'est-à-dire sin(x) = sin(x + 2π) = sin(x + 4π) et ainsi de suite. Cependant, bien entendu, les fonctions trigonométriques ne sont pas les seules fonctions périodiques.

Pour les fonctions simples et basiques, la seule façon de déterminer si elles sont périodiques ou non périodiques est le calcul. Mais pour les fonctions complexes, il existe déjà plusieurs règles simples.

Si F(x) est de période T et qu'une dérivée est définie pour elle, alors cette dérivée f(x) = F′(x) est également une fonction périodique de période T. Après tout, la valeur de la dérivée au point x est égal à la tangente de l'angle tangentiel du graphique de sa primitive en ce point à l'axe des x, et puisque la primitive se répète périodiquement, la dérivée doit également se répéter. Par exemple, la dérivée de la fonction sin(x) est égale à cos(x) et elle est périodique. Prendre la dérivée de cos(x) vous donne –sin(x). La fréquence reste inchangée.

Cependant, l’inverse n’est pas toujours vrai. Ainsi, la fonction f(x) = const est périodique, mais sa primitive F(x) = const*x + C ne l'est pas.

Si F(x) est une fonction périodique de période T, alors G(x) = a*F(kx + b), où a, b et k sont des constantes et k n'est pas égal à zéro - est également une fonction périodique , et sa période est T/k. Par exemple, sin(2x) est une fonction périodique et sa période est π. Cela peut être représenté visuellement comme suit : en multipliant x par un certain nombre, vous semblez compresser le graphique de la fonction horizontalement exactement autant de fois

Si F1(x) et F2(x) sont des fonctions périodiques et que leurs périodes sont respectivement égales à T1 et T2, alors la somme de ces fonctions peut également être périodique. Toutefois, sa période ne sera pas une simple somme des périodes T1 et T2. Si le résultat de la division T1/T2 est un nombre rationnel, alors la somme des fonctions est périodique et sa période est égale au plus petit commun multiple (LCM) des périodes T1 et T2. Par exemple, si la période de la première fonction est de 12 et la période de la seconde de 15, alors la période de leur somme sera égale à LCM (12, 15) = 60.

Cela peut être représenté visuellement comme suit : les fonctions ont différentes « largeurs de pas », mais si le rapport de leurs largeurs est rationnel, alors tôt ou tard (ou plutôt, précisément grâce au LCM des pas), elles redeviendront égales, et leur somme entamera une nouvelle période.

Cependant, si le rapport des périodes est irrationnel, alors la fonction totale ne sera pas du tout périodique. Par exemple, soit F1(x) = x mod 2 (le reste lorsque x est divisé par 2) et F2(x) = sin(x). T1 sera ici égal à 2, et T2 sera égal à 2π. Le rapport des périodes est égal à π - un nombre irrationnel. Par conséquent, la fonction sin(x) + x mod 2 n’est pas périodique.

Objectif : résumer et systématiser les connaissances des étudiants sur le thème « Périodicité des fonctions » ; développer des compétences pour appliquer les propriétés d'une fonction périodique, trouver la plus petite période positive d'une fonction, construire des graphiques de fonctions périodiques ; promouvoir l'intérêt pour l'étude des mathématiques ; cultiver l’observation et la précision.

Équipement : ordinateur, projecteur multimédia, fiches de tâches, diapositives, horloges, tables d'ornements, éléments d'artisanat populaire

« Les mathématiques sont ce que les gens utilisent pour contrôler la nature et eux-mêmes. »
UN. Kolmogorov

Pendant les cours

I. Étape organisationnelle.

Vérifier l'état de préparation des élèves pour la leçon. Rapportez le sujet et les objectifs de la leçon.

II. Vérification des devoirs.

Nous vérifions les devoirs à l'aide d'échantillons et discutons des points les plus difficiles.

III. Généralisation et systématisation des connaissances.

1. Travail frontal oral.

Problèmes de théorie.

1) Former une définition de la durée de la fonction
2) Nommer la plus petite période positive des fonctions y=sin(x), y=cos(x)
3). Quelle est la plus petite période positive des fonctions y=tg(x), y=ctg(x)
4) À l'aide d'un cercle, prouvez l'exactitude des relations :

y=péché(x) = péché(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18 0º)
y=ctg(x) = ctg(x+180º)

tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z

5) Comment tracer une fonction périodique ?

Exercices oraux.

1) Démontrer les relations suivantes

un) péché(740º) = péché(20º)
b) cos(54º) = cos(-1026º)
c) péché(-1000º) = péché(80º)

2. Montrer qu'un angle de 540º est l'une des périodes de la fonction y= cos(2x)

3. Montrer qu'un angle de 360º est l'une des périodes de la fonction y=tg(x)

4. Transformez ces expressions pour que les angles qu'elles contiennent ne dépassent pas 90º en valeur absolue.

un) tg375º
b) ctg530º
c) péché1268º
d) cos(-7363º)

5. Où avez-vous rencontré les mots PÉRIODE, PÉRIODICITÉ ?

Réponses de l'élève : Une période en musique est une structure dans laquelle est présentée une pensée musicale plus ou moins complète. Une période géologique fait partie d'une époque et est divisée en époques d'une période de 35 à 90 millions d'années.

Demi-vie d'une substance radioactive. Fraction périodique. Les périodiques sont des publications imprimées qui paraissent dans des délais strictement définis. Le système périodique de Mendeleïev.

6. Les figures montrent des parties de graphiques de fonctions périodiques. Déterminez la période de la fonction. Déterminez la période de la fonction.

Répondre:T=2; T = 2 ; T = 4 ; T=8.

7. Où dans votre vie avez-vous rencontré la construction d'éléments répétitifs ?

Réponse de l'élève : Éléments d'ornements, art populaire.

IV. Résolution collective de problèmes.

(Résoudre des problèmes sur les diapositives.)

Considérons l'une des façons d'étudier une fonction de périodicité.

Cette méthode évite les difficultés liées à la preuve qu'une période particulière est la plus petite et élimine également le besoin d'aborder des questions sur les opérations arithmétiques sur les fonctions périodiques et la périodicité d'une fonction complexe. Le raisonnement repose uniquement sur la définition d'une fonction périodique et sur le fait suivant : si T est la période de la fonction, alors nT(n?0) est sa période.

Problème 1. Trouver la plus petite période positive de la fonction f(x)=1+3(x+q>5)

Solution : Supposons que la période T de cette fonction. Alors f(x+T)=f(x) pour tout x € D(f), c'est-à-dire

1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0,25)

Mettons x=-0,25 on obtient

(T)=0<=>T=n, n€Z

Nous avons obtenu que toutes les périodes de la fonction en question (si elles existent) sont parmi les entiers. Choisissons le plus petit nombre positif parmi ces nombres. Ce 1 . Vérifions si ce sera réellement une période 1 .

f(x+1) =3(x+1+0,25)+1

Puisque (T+1)=(T) pour tout T, alors f(x+1)=3((x+0.25)+1)+1=3(x+0.25)+1=f(x ), c'est-à-dire 1 – période f. Puisque 1 est le plus petit de tous les entiers positifs, alors T=1.

Problème 2. Montrer que la fonction f(x)=cos 2 (x) est périodique et trouver sa période principale.

Problème 3. Trouver la période principale de la fonction

f(x)=sin(1,5x)+5cos(0,75x)

Supposons la période T de la fonction, alors pour tout X le rapport est valable

sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)

Si x=0, alors

péché(1,5T)+5cos(0,75T)=sin0+5cos0

péché(1,5T)+5cos(0,75T)=5

Si x=-T, alors

sin0+5cos0=sin(-1,5T)+5cos0,75(-T)

5= – péché(1,5T)+5cos(0,75T)

péché(1,5T)+5cos(0,75T)=5 – sin(1,5T)+5cos(0,75T)=5

En additionnant, on obtient :

10cos(0,75T)=10

2π n, n € Z

Choisissons le plus petit nombre positif parmi tous les nombres « suspects » pour la période et vérifions s'il s'agit d'une période pour f. Ce nombre

f(x+)=sin(1,5x+4π )+5cos(0,75x+2π )= sin(1,5x)+5cos(0,75x)=f(x)

Cela signifie qu'il s'agit de la période principale de la fonction f.

Problème 4. Vérifions si la fonction f(x)=sin(x) est périodique

Soit T la période de la fonction f. Alors pour tout x

péché|x+Т|=péché|x|

Si x=0, alors sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.

Assumons. Que pour certains n le nombre π n est la période

la fonction considérée π n>0. Alors sin|π n+x|=sin|x|

Cela implique que n doit être à la fois un nombre pair et un nombre impair, mais cela est impossible. Cette fonction n’est donc pas périodique.

Tâche 5. Vérifier si la fonction est périodique

f(x)=

Soit T la période de f, alors

, donc sinT=0, Т=π n, n € Z. Supposons que pour un certain n le nombre π n soit bien la période de cette fonction. Alors le nombre 2π n sera la période

Puisque les numérateurs sont égaux, leurs dénominateurs sont égaux, donc

Cela signifie que la fonction f n'est pas périodique.

Travaillez en groupe.

Tâches pour le groupe 1.

Tâches pour le groupe 2.

Vérifiez si la fonction f est périodique et trouvez sa période fondamentale (si elle existe).

f(x)=cos(2x)+2sin(2x)

Tâches pour le groupe 3.

A la fin de leurs travaux, les groupes présentent leurs solutions.

VI. Résumer la leçon.

Réflexion.

L'enseignant remet aux élèves des fiches avec des dessins et leur demande de colorier une partie du premier dessin en fonction de leur degré de maîtrise des méthodes d'étude d'une fonction de périodicité, et une partie du deuxième dessin - en fonction de leur contribution au travail de la leçon.

VII. Devoirs

1). Vérifier si la fonction f est périodique et trouver sa période fondamentale (si elle existe)

b). f(x)=x 2 -2x+4

c). f(x)=2tg(3x+5)

2). La fonction y=f(x) a une période T=2 et f(x)=x 2 +2x pour x € [-2; 0]. Trouver la valeur de l'expression -2f(-3)-4f(3.5)

Littérature/

1. Mordkovitch A.G. Algèbre et débuts de l'analyse avec étude approfondie.
2. Mathématiques. Préparation à l'examen d'État unifié. Éd. Lysenko F.F., Kulabukhova S.Yu.
3. Cheremetieva T.G. , Tarasova E.A. Algèbre et analyse initiale pour les classes 10-11.