The binomial distribution is one of the most important probability distributions of a discretely varying random variable. The binomial distribution is the probability distribution of the number m occurrence of an event A V n mutually independent observations. Often an event A is called the “success” of an observation, and the opposite event is called “failure,” but this designation is very conditional.

Conditions binomial distribution :

• V total carried out n trials in which the event A may or may not occur;
• event A in each test can occur with the same probability p;
• tests are mutually independent.

The probability that in n testing event A it will come exactly m times, can be calculated using Bernoulli's formula:

,

Where p- probability of an event occurring A;

q = 1 - p- the probability of the opposite event occurring.

Let's figure it out why is the binomial distribution related to Bernoulli's formula in the manner described above? . Event - number of successes at n tests are divided into a number of options, in each of which success is achieved in m tests, and failure - in n - m tests. Let's consider one of these options - B1 . Using the rule for adding probabilities, we multiply the probabilities of opposite events:

,

and if we denote q = 1 - p, That

.

Any other option in which m success and n - m failures. The number of such options is equal to the number of ways in which one can n test get m success.

Sum of all probabilities m event occurrence numbers A(numbers from 0 to n) is equal to one:

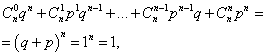
where each term represents a term in Newton's binomial. Therefore, the distribution under consideration is called the binomial distribution.

In practice, it is often necessary to calculate probabilities "no more than m success in n tests" or "at least m success in n tests". The following formulas are used for this.

The integral function, that is probability F(m) what's in n observational event A no more will come m once, can be calculated using the formula:

In its turn probability F(≥m) what's in n observational event A will come no less m once, is calculated by the formula:

Sometimes it is more convenient to calculate the probability that n observational event A no more will come m times, through the probability of the opposite event:

.

Which formula to use depends on which of them has the sum containing fewer terms.

The characteristics of the binomial distribution are calculated using the following formulas .

Expected value: .

Dispersion: .

Standard deviation: .

Binomial distribution and calculations in MS Excel

Binomial probability P n ( m) and the values ​​of the integral function F(m) can be calculated using the MS Excel function BINOM.DIST. The window for the corresponding calculation is shown below (left click to enlarge).

MS Excel requires you to enter the following data:

• number of successes;
• number of tests;
• probability of success;
• integral - logical value: 0 - if you need to calculate the probability P n ( m) and 1 - if the probability F(m).

Example 1. The company manager summarized information on the number of cameras sold over the last 100 days. The table summarizes the information and calculates the probabilities that a certain number of cameras will be sold per day.

The day ends with a profit if 13 or more cameras are sold. Probability that the day will be worked out profitably:

Probability that a day will be worked without profit:

Let the probability that a day is worked with a profit be constant and equal to 0.61, and the number of cameras sold per day does not depend on the day. Then we can use the binomial distribution, where the event A- the day will be worked with profit, - without profit.

Probability that all 6 days will be worked out with profit:

.

We get the same result using the MS Excel function BINOM.DIST (the value of the integral value is 0):

P 6 (6 ) = BINOM.DIST(6; 6; 0.61; 0) = 0.052.

The probability that out of 6 days 4 and more days will be worked out at a profit:

Where ,

,

Using the MS Excel function BINOM.DIST, we calculate the probability that out of 6 days no more than 3 days will be completed with a profit (the value of the integral value is 1):

P 6 (≤3 ) = BINOM.DIST(3; 6; 0.61; 1) = 0.435.

Probability that all 6 days will be worked out with losses:

,

We can calculate the same indicator using the MS Excel function BINOM.DIST:

P 6 (0 ) = BINOM.DIST(0; 6; 0.61; 0) = 0.0035.

Solve the problem yourself and then see the solution

Example 2. There are 2 white balls and 3 black balls in the urn. A ball is taken out of the urn, the color is set and put back. The attempt is repeated 5 times. The number of occurrences of white balls is a discrete random variable X, distributed according to the binomial law. Draw up a law of distribution of a random variable. Define mode, mathematical expectation and dispersion.

Let's continue to solve problems together

Example 3. From the courier service we went to the sites n= 5 couriers. Each courier is likely p= 0.3, regardless of others, is late for the object. Discrete random variable X- number of late couriers. Construct a distribution series for this random variable. Find its mathematical expectation, variance, standard deviation. Find the probability that at least two couriers will be late for the objects.

Despite their exotic names, common distributions relate to each other in intuitive and interesting ways that make them easy to remember and reason about with confidence. Some follow naturally, for example, from the Bernoulli distribution. Time to show a map of these connections.

Each distribution is illustrated by an example of its distribution density function (DFF). This article is only about those distributions whose outcomes are single numbers. Therefore, the horizontal axis of each graph is a set of possible outcome numbers. Vertical – the probability of each outcome. Some distributions are discrete - their outcomes must be integers, such as 0 or 5. These are indicated by sparse lines, one for each outcome, with a height corresponding to the probability of a given outcome. Some are continuous, their outcomes can take on any numerical value, such as -1.32 or 0.005. These are shown as dense curves with areas under the sections of the curve that give probabilities. The sum of the heights of lines and areas under curves is always 1.

Print, cut according dotted line and carry it with you in your wallet. This is your guide to the country of distributions and their relatives.

Bernoulli and uniform

You have already encountered the Bernoulli distribution above, with two outcomes - heads or tails. Imagine it now as a distribution over 0 and 1, 0 is heads, 1 is tails. As is already clear, both outcomes are equally likely, and this is reflected in the diagram. The Bernoulli PDF contains two lines of equal height, representing 2 equally probable outcomes: 0 and 1, respectively.

The Bernoulli distribution can also represent unequally probable outcomes, such as flipping an incorrect coin. Then the probability of heads will not be 0.5, but some other value p, and the probability of tails will be 1-p. Like many other distributions, this is actually a whole family of distributions given by certain parameters, as p above. When you think “Bernoulli”, think about “tossing a (possibly wrong) coin.”

From here it is a very small step to represent the distribution on top of several equally probable outcomes: a uniform distribution characterized by a flat PDF. Imagine a regular dice. Its outcomes 1-6 are equally probable. It can be specified for any number of outcomes n, and even as a continuous distribution.

Think of an even distribution as a “straight die.”

Binomial and hypergeometric

The binomial distribution can be thought of as the sum of the outcomes of those things that follow the Bernoulli distribution.

Toss a fair coin twice - how many times will it be heads? This is a number that follows the binomial distribution. Its parameters are n, the number of trials, and p – the probability of “success” (in our case, heads or 1). Each throw is a Bernoulli-distributed outcome, or test. Use the binomial distribution when counting the number of successes in things like tossing a coin, where each toss is independent of the others and has the same probability of success.

Or imagine an urn with the same number of white and black balls. Close your eyes, take out the ball, write down its color and put it back. Repeat. How many times is the black ball drawn? This number also follows the binomial distribution.

We presented this strange situation to make it easier to understand the meaning of the hypergeometric distribution. This is the distribution of the same number, but in the situation if we Not returned the balls. It certainly cousin binomial distribution, but not the same, since the probability of success changes with each ball drawn. If the number of balls is large enough compared to the number of draws, then these distributions are almost identical, since the chance of success changes extremely slightly with each draw.

When someone talks about pulling balls out of urns without returning them, it is almost always safe to say “yes, hypergeometric distribution,” because I have never met anyone in my life who actually filled urns with balls and then pulled them out and returned them, or vice versa. I don’t even know anyone with trash cans. Even more often, this distribution should emerge when selecting a significant subset of some population as a sample.

Note translation

It may not be very clear here, but since the tutorial is an express course for beginners, it should be clarified. The population is something that we want to statistically evaluate. To estimate, we select a certain part (subset) and make the required estimate on it (then this subset is called a sample), assuming that the estimate for the entire population will be similar. But for this to be true, additional restrictions are often required on the definition of a subset of the sample (or, conversely, given a known sample, we need to evaluate whether it sufficiently accurately describes the population).

A practical example - we need to select representatives from a company of 100 people to travel to E3. It is known that 10 people already traveled there last year (but no one admits it). How much minimum do you need to take so that there is a high probability of at least one experienced comrade in the group? In this case population- 100, sample - 10, sample requirements - at least one who has already been to E3.

Wikipedia has a less funny, but more practical example about defective parts in a batch.

Poisson

What about the number of customers calling hotline to technical support every minute? This is an outcome whose distribution appears to be binomial, if we count each second as a Bernoulli test during which the customer either does not call (0) or calls (1). But power supply organizations know very well: when the electricity is turned off, two people can call in a second. or even more than a hundred of people. Thinking of it as 60,000 millisecond tests doesn't help either - there are more tests, the probability of a call per millisecond is less, even if you don't count two or more at the same time, but, technically, this is still not a Bernoulli test. However, it works logical reasoning with the transition to infinity. Let n tend to infinity and p to 0, so that np is constant. It's like dividing into smaller and smaller fractions of time with an increasingly smaller probability of a call. In the limit we get the Poisson distribution.

Just like the binomial, the Poisson distribution is a count distribution: the number of times something will happen. It is parameterized not by the probability p and the number of trials n, but by the average intensity λ, which, in analogy with the binomial, is simply a constant value np. Poisson distribution - what it's all about necessary remember when we are talking about counting events over a certain time at a constant given intensity.

When there is something, such as packets arriving at a router, or customers appearing in a store, or something waiting in line, think “Poisson”.

Geometric and negative binomial

From simple Bernoulli tests a different distribution emerges. How many times will a coin land heads before it lands on heads? The number of tails follows a geometric distribution. Like the Bernoulli distribution, it is parameterized by the probability of a successful outcome, p. It is not parameterized by the number n, the number of throw-tests, because the number of unsuccessful tests is precisely the outcome.

If the binomial distribution is “how many successes,” then the geometric distribution is “How many failures before success?”

The negative binomial distribution is a simple generalization of the previous one. This is the number of failures before there are r, not 1, successes. Therefore, it is further parameterized by this r. It is sometimes described as the number of successes to r failures. But as my life coach says: “You decide what is success and what is failure,” so it’s the same thing, as long as you remember that the probability p should also be the correct probability of success or failure, respectively.

If you need a joke to relieve the tension, you can mention that the binomial and hypergeometric distributions are an obvious pair, but the geometric and negative binomial are also quite similar, and then say, “Well, who calls them all that, huh?”

Exponential and Weibula

Again about calls to technical support: how long will it take until the next call? The distribution of this waiting time seems to be geometric, because every second until no one calls is like a failure, until the second until the call finally occurs. The number of failures is like the number of seconds until no one called, and this practically time until the next call, but “practically” is not enough for us. The point is that this time will be the sum of whole seconds, and, thus, it will not be possible to count the wait within this second before the call itself.

Well, as before, we move to the limit in the geometric distribution, regarding time shares - and voila. We obtain an exponential distribution that accurately describes the time before the call. This is a continuous distribution, the first of our kind, because the outcome is not necessarily in whole seconds. Like the Poisson distribution, it is parameterized by the intensity λ.

Reiterating the connection between the binomial and the geometric, Poisson's “how many events in time?” is related to the exponential “how long before the event?” If there are events whose number per unit time obeys the Poisson distribution, then the time between them obeys the exponential distribution with the same parameter λ. This correspondence between the two distributions must be noted when either of them is discussed.

The exponential distribution should come to mind when thinking about "time to event", perhaps "time to failure". In fact, this is such an important situation that more generalized distributions exist to describe MTBF, such as the Weibull distribution. While the exponential distribution is appropriate when the wear rate, or failure rate, for example, is constant, the Weibull distribution can model failure rates increasing (or decreasing) over time. Exponential is, in general, a special case.

Think "Weibull" when talking about MTBF.

Normal, lognormal, Student's t and chi-square

The normal, or Gaussian, distribution is probably one of the most important. Its bell-shaped shape is immediately recognizable. Like , this is a particularly curious entity that manifests itself everywhere, even from the most seemingly simple sources. Take a set of values ​​that follow the same distribution - any one! - and fold them. The distribution of their sum follows (approximately) a normal distribution. The more things are added up, the closer their sum corresponds to the normal distribution (the catch: the distribution of terms must be predictable, independent, it tends only to normal). That this is true despite the original distribution is amazing.

Note translation

I was surprised that the author does not write about the need for a comparable scale of summed distributions: if one significantly dominates the others, convergence will be extremely bad. And, in general, absolute mutual independence is not necessary; weak dependence is sufficient.

Well, probably good for parties, as he wrote.

This is called the “central limit theorem”, and you need to know what it is, why it is called that and what it means, otherwise you will instantly laugh.

In its context, normal is associated with all distributions. Although, basically, it is associated with the distribution of all sorts of amounts. The sum of Bernoulli trials follows a binomial distribution and, as the number of trials increases, this binomial distribution becomes closer to a normal distribution. Likewise, its cousin is the hypergeometric distribution. The Poisson distribution - the limiting form of the binomial - also approaches normal with increasing intensity parameter.

Outcomes that follow a lognormal distribution produce values ​​whose logarithm is normally distributed. Or in other words: the exponent of a normally distributed value is lognormally distributed. If the sums are normally distributed, then remember that the products are lognormally distributed.

The Student t distribution is the basis of the t test, which many non-statisticians study in other fields. It is used to make assumptions about the mean of a normal distribution and also tends to the normal distribution as its parameter increases. Distinctive feature t-distribution - its tails, which are thicker than those of the normal distribution.

If the fat-tailed joke didn't rock your neighbor enough, move on to a rather funny tale about beer. More than 100 years ago, Guinness used statistics to improve its stout. Then William Seely Gosset invented a completely new statistical theory for improved barley cultivation. Gossett convinced his boss that other brewers would not understand how to use his ideas, and received permission to publish, but under the pseudonym "Student". The most famous achievement Gosset - this is precisely the t-distribution, which, one might say, is named after him.

Finally, the chi-square distribution is the distribution of sums of squares of normally distributed values. The chi-square test is based on this distribution, which itself is based on the sum of squares of the differences, which should be normally distributed.

Gamma and beta

At this point, if you have already started talking about something chi-square, the conversation begins in earnest. You may already be talking to real statisticians, and you should probably bow out already, because things like the gamma distribution may come up. This is a generalization And exponential And chi-square distribution. Like the exponential distribution, it is used for complex models waiting times. For example, a gamma distribution appears when the time to the next n events is simulated. It appears in machine learning as the “adjoint prior distribution” to a couple of other distributions.

Don't talk about these conjugate distributions, but if you have to, don't forget to talk about the beta distribution, because it is the conjugate prior to most of the distributions mentioned here. Data scientists are sure that this is exactly what it was made for. Mention this casually and go to the door.

The beginning of wisdom

Probability distributions are something you can't know too much about. The truly interested can refer to this super-detailed map of all probability distributions Add tags

Probability distribution is a probability measure on a measurable space.

Let W be a non-empty set of arbitrary nature and Ƒ -s- algebra on W, that is, a collection of subsets of W containing W itself, the empty set Æ, and closed under at most a countable set of set-theoretic operations (this means that for any A Î Ƒ set = W\ A belongs again Ƒ and if A 1 , A 2 ,…О Ƒ , That Ƒ And Ƒ ). Pair (W, Ƒ ) is called a measurable space. Non-negative function P( A), defined for everyone A Î Ƒ , is called a probability measure, probability, P. probabilities or simply P., if P(W) = 1 and P is countably additive, that is, for any sequence A 1 , A 2 ,…О Ƒ such that A i ∩ A j= Æ for all i ¹ j, the equality P() = P( A i). Three (W, Ƒ , P) is called a probability space. Probability space is the original concept of the axiomatic probability theory proposed by A.N. Kolmogorov in the early 1930s.

On every probability space one can consider (real) measurable functions X = X(w), wÎW, that is, functions such that (w: X(w)О B} Î Ƒ for any Borel subset B real line R. Measurability of a function X is equivalent to (w: X(w)< x} Î Ƒ for any real x. Measurable functions are called random variables. Each random variable X, defined on the probability space (W, Ƒ , P), generates P. probabilities

P X (B) = P( XÎ B) = P((w: X(w)О B}), B Î Ɓ ,
on measurable space ( R, Ɓ ), Where Ɓ R, and the distribution function

F X(x) = P( X < x) = P((w: X(w)< x}), -¥ < x <¥,
which are called probability probability and distribution function of a random variable X.

Distribution function F any random variable has the properties

1. F(x) non-decreasing,

2. F(- ¥) = 0, F(¥) = 1,

3. F(x) is left continuous at every point x.

Sometimes in the definition of the distribution function the inequality< заменяется неравенством £; в этом случае функция распределения является непрерывной справа. В содержательных утверждениях теории вероятностей не важно, непрерывна функция распределения слева или справа, важны лишь положения ее точек разрыва x(if any) and increment sizes F(x+0) - F(x-0) at these points; If F X, then this increment is P( X = x).

Any function F, having properties 1. - 3. is called a distribution function. Correspondence between distributions on ( R, Ɓ ) and distribution functions are one-to-one. For any R. P on ( R, Ɓ ) its distribution function is determined by the equality F(x) = P((-¥, x)), -¥ < x <¥, а для любой функции распределения F corresponding to it R. P is defined on the algebra £ of sets consisting of unions of a finite number of disjoint intervals function F 1 (x) increases linearly from 0 to 1. To construct the function F 2 (x) the segment is divided into segment , interval (1/3, 2/3) and segment . Function F 2 (x) on the interval (1/3, 2/3) is equal to 1/2 and increases linearly from 0 to 1/2 and from 1/2 to 1 on the segments and, respectively. This process continues and the function Fn+1 is obtained using the following function transformation Fn, n³ 2. On intervals where the function Fn(x) is constant, Fn +1 (x) coincides with Fn(x). Each segment where the function Fn(x) increases linearly from a before b, is divided into segment , interval (a + (a - b)/3, a + 2(b - a)/3) and segment . At the specified interval Fn +1 (x) is equal to ( a + b)/2, and on the indicated segments Fn +1 (x) increases linearly from a before ( a + b)/2and from ( a + b)/2 to b respectively. For each 0 £ x£1 sequence Fn(x), n= 1, 2,..., converges to some number F(x). Sequence of distribution functions Fn, n= 1, 2,..., is equicontinuous, therefore the limit distribution function F(x) is continuous. This function is constant on a countable set of intervals (the values ​​of the function are different on different intervals), on which there are no growth points, and the total length of these intervals is 1. Therefore, the Lebesgue measure of the set supp F is equal to zero, that is F singular.

Each distribution function can be represented as

F(x) = p ac F ac ( x) + p d F d ( x) + p s F s ( x),
Where F ac, F d and F s is absolutely continuous, discrete and singular distribution functions, and the sum of non-negative numbers p ac, p d and p s is equal to one. This representation is called the Lebesgue expansion, and the functions F ac, F d and F s - components of decomposition.

The distribution function is called symmetric if F(-x) = 1 - F(x+ 0) for
x> 0. If a symmetric distribution function is absolutely continuous, then its density is an even function. If the random variable X has a symmetric distribution, then the random variables X And - X equally distributed. If the symmetric distribution function F(x) is continuous at zero, then F(0) = 1/2.

Among the absolutely continuous rules often used in probability theory are uniform rules, normal rules (Gauss rules), exponential rules, and Cauchy rules.

R. is called uniform on the interval ( a, b) (or on the segment [ a, b], or at intervals [ a, b) And ( a, b]), if its density is constant (and equal to 1/( b - a)) on ( a, b) and equal to zero outside ( a, b). Most often, a uniform distribution on (0, 1) is used, its distribution function F(x) is equal to zero at x£ 0, equal to one at x>1 and F(x) = x at 0< x£ 1. A uniform random variable on (0, 1) has X(w) = w on a probability space consisting of the interval (0, 1), a set of Borel subsets of this interval and the Lebesgue measure. This probability space corresponds to the experiment “throwing a point w at random onto the interval (0, 1)”, where the word “at random” means equality (“equal opportunity”) of all points from (0, 1). If on the probability space (W, Ƒ , P) there is a random variable X with a uniform distribution on (0, 1), then on it for any distribution function F there is a random variable Y, for which the distribution function F Y coincides with F. For example, the distribution function of a random variable Y = F -1 (X) coincides with F. Here F -1 (y) = inf( x: F(x) > y}, 0 < y < 1; если функция F(x) is continuous and strictly monotone on the entire real line, then F-1 - inverse function F.

Normal R. with parameters ( a, s 2), -¥< a < ¥, s 2 >0, called R. with density, -¥< x < ¥. Чаще всего используется нормальное Р. с параметрами a= 0 and s 2 = 1, which is called standard normal R., its distribution function F( x) is not expressed through superpositions of elementary functions and we have to use its integral representation F( x) =, -¥ < x < ¥. Для фунции распределения F(x) detailed tables were compiled that were necessary before modern computing technology appeared (values ​​of the function F( x) can also be obtained using special tables. functions erf( x)), values ​​F( x) For x> 0 can be obtained using the sum of the series

,
and for x < 0 можно воспользоваться симметричностью F(x). Normal distribution function values ​​with parameters a and s 2 can be obtained using the fact that it coincides with F(( x - a)/s). If X 1 and X 2 independent normally distributed with parameters a 1 , s 1 2 and a 2 , s 2 2 random variables, then the distribution of their sum X 1 + X 2 is also ok with parameters a= a 1 + a 2 and s 2 = s 1 2 + s 2 2 . The statement is also true, in a sense, the opposite: if a random variable X normally distributed with parameters a and s 2 and
X = X 1 + X 2 where X 1 and X 2 are independent random variables other than constants, then X 1 and X 2 have normal distributions (Cramer’s theorem). Options a 1 , s 1 2 and a 2 , s 2 2 distributions of normal random variables X 1 and X 2 related to a and s 2 by the equalities given above. Standard normal distribution is the limit in the central limit theorem.

Exponential distribution is a distribution with density p(x) = 0 at x < 0 и p(x) = l e- l x at x³ 0, where l > 0 is a parameter, its distribution function F(x) = 0 at x£0 and F(x) = 1 - e- l x at x> 0 (sometimes exponential parameters are used, which differ from the indicated one by a shift along the real axis). This R. has a property called the absence of aftereffect: if X is a random variable with exponential R., then for any positive x And t

P( X > x + t | X > x) = P( X > t).
If X is the operating time of some device before failure, then the absence of aftereffect means that the probability that the device, turned on at time 0, will not fail until x + t provided that he did not refuse until the moment x, does not depend on x. This property is interpreted as the absence of "aging". The absence of aftereffect is a characteristic property of exponential distribution: in the class of absolutely continuous distributions, the above equality is valid only for exponential distribution (with some parameter l > 0). Exponential R. appears as a limit R. in the minimum scheme. Let X 1 , X 2 ,… - non-negative independent identically distributed random variables and for their common distribution function F point 0 is the growth point. Then at n®¥ distributions of random variables Yn= min( X 1 ,…, Xn) weakly converge to a degenerate distribution with a single growth point 0 (this is an analogue of the law large numbers). If we additionally assume that for some e > 0 the distribution function F(x) on the interval (0, e) admits representation and p(u)®l at u¯ 0, then the distribution functions of random variables Z n = n min( X 1 ,…, Xn) at n®¥ evenly across -¥< x < ¥ сходятся к экспоненциальной функции распределения с параметром l (это - аналог центральной предельной теоремы).

R. Cauchy is called R. with density p(x) = 1/(p(1 + x 2)), -¥< x < ¥, его функция рас-пределения F(x) = (arctg x+ p/2)/p. This R. appeared in the work of S. Poisson in 1832 in connection with the solution of the following problem: are there independent identically distributed random variables? X 1 , X 2 ,... such that the arithmetic means ( X 1 + … + Xn)/n at every n have the same R. as each of the random variables X 1 , X 2 ,...? S. Poisson discovered that random variables with the specified density have this property. For these random variables, the statement of the law of large numbers does not hold, in which arithmetic means ( X 1 +…+ Xn)/n with growth n degenerate. However, this does not contradict the law of large numbers, since it imposes restrictions on the distributions of the original random variables that are not satisfied for the specified distribution (for this distribution there are absolute moments of all positive orders less than unity, but the mathematical expectation does not exist) . In the works of O. Cauchy, R., bearing his name, appeared in 1853. R. Cauchy is related X/Y independent random variables with standard normal P.

Among the discrete variables often used in probability theory are R. Bernoulli, binomial R. and R. Poisson.

R. Bernoulli calls any distribution with two growth points. The most commonly used random variable is R. X, taking values ​​0 and 1 with probabilities
q = 1 - p And p respectively, where 0< p < 1 - параметр. Первые формы закона больших чисел и центральной предельной теоремы были получены для случайных величин, имею-щих Р. Бернулли. Если на вероятностном пространстве (W, Ƒ , P) there is a sequence X 1 , X 2,... independent random variables taking values ​​0 and 1 with probabilities of 1/2 each, then on this probability space there exists a random variable with uniform R on (0, 1). In particular, the random variable has a uniform distribution on (0, 1).

Binomial R. with parameters n And p, n- natural, 0< p < 1, называется Р., с точками роста 0, 1,..., n, in which the probabilities are concentrated C n k p k q n-k, k = 0, 1,…, n,
q = 1 - p. It is R. amount n independent random variables having R. Bernoulli with growth points 0 and 1, in which the probabilities are concentrated q And p. The study of this distribution led J. Bernoulli to the discovery of the law of large numbers, and A. Moivre to the discovery of the central limit theorem.

A Poisson formula is called a formula whose support is a sequence of points 0, 1,..., in which the probabilities l are concentrated k e-l/ k!, k= 0, 1,…, where l > 0 is a parameter. The sum of two independent random variables having a R. Poisson with parameters l and m again has a R. Poisson with the parameter l + m. R. Poisson is the limit for R. Bernoulli with parameters n And p = p(n) at n®¥ if n And p related by the relation n.p.®l at n®¥ (Poisson's theorem). If the sequence is 0< T 1 < T 2 < T 3 <… есть последовательность моментов времени, в которые происходят некоторые события (так. наз поток событий) и величины T 1 , T 2 -T 1 , T 3 - T 2 ,... are independent identically distributed random variables and their common R. is exponential with parameter l > 0, then the random variable X t, equal to the number of events that occurred in the interval (0, t), has R. Poisson with parameter.l t(such a flow is called Poisson).

The concept of R has numerous generalizations; in particular, it extends to the multidimensional case and to algebraic structures.

As is known, random variable is called a variable quantity that can take on certain values ​​depending on the case. Random variables are denoted by capital letters of the Latin alphabet (X, Y, Z), and their values ​​are denoted by corresponding lowercase letters (x, y, z). Random variables are divided into discontinuous (discrete) and continuous.

Discrete random variable is a random variable that takes only a finite or infinite (countable) set of values ​​with certain non-zero probabilities.

Distribution law of a discrete random variable is a function that connects the values ​​of a random variable with their corresponding probabilities. The distribution law can be specified in one of the following ways.

1 . The distribution law can be given by the table:

where λ>0, k = 0, 1, 2, … .

V) by using distribution functions F(x) , which determines for each value x the probability that the random variable X will take a value less than x, i.e. F(x) = P(X< x).

Properties of the function F(x)

3 . The distribution law can be specified graphically – distribution polygon (polygon) (see problem 3).

Note that to solve some problems it is not necessary to know the distribution law. In some cases, it is enough to know one or more numbers that reflect the most important features law of distribution. This can be a number that has the meaning of the “average value” of a random variable, or a number showing the average size of the deviation of a random variable from its mean value.

Numbers of this kind are called numerical characteristics of a random variable. :

• Basic numerical characteristics of a discrete random variable Mathematical expectation (average value) of a discrete random variable.
  M(X)=Σ x i p i
• For binomial distribution M(X)=np, for Poisson distribution M(X)=λ Dispersion discrete random variable D(X)=M2 or D(X) = M(X 2)− 2
  . The difference X–M(X) is called the deviation of a random variable from its mathematical expectation.
• For binomial distribution D(X)=npq, for Poisson distribution D(X)=λ (Standard deviation) standard deviation.

σ(X)=√D(X)

Examples of solving problems on the topic “The law of distribution of a discrete random variable”

Task 1. 1000 released lottery tickets

: for 5 of them there is a winning of 500 rubles, for 10 – a winning of 100 rubles, for 20 – a winning of 50 rubles, for 50 – a winning of 10 rubles. Determine the law of probability distribution of the random variable X - winnings per ticket. Solution.

According to the conditions of the problem, the following values ​​of the random variable X are possible: 0, 10, 50, 100 and 500.

The number of tickets without winning is 1000 – (5+10+20+50) = 915, then P(X=0) = 915/1000 = 0.915.

Similarly, we find all other probabilities: P(X=0) = 50/1000=0.05, P(X=50) = 20/1000=0.02, P(X=100) = 10/1000=0.01 , P(X=500) = 5/1000=0.005. Let us present the resulting law in the form of a table:

Let's find the mathematical expectation of the value X: M(X) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+ 2+3+4+5+6)/6 = 21/6 = 3.5

The device consists of three independently operating elements.

: for 5 of them there is a winning of 500 rubles, for 10 – a winning of 100 rubles, for 20 – a winning of 50 rubles, for 50 – a winning of 10 rubles. Determine the law of probability distribution of the random variable X - winnings per ticket. 1. The probability of failure of each element in one experiment is 0.1. Draw up a distribution law for the number of failed elements in one experiment, construct a distribution polygon. Find the distribution function F(x) and plot it. Find the mathematical expectation, variance and standard deviation of a discrete random variable.

The discrete random variable X = (the number of failed elements in one experiment) has the following possible values: x 1 = 0 (none of the device elements failed), x 2 = 1 (one element failed), x 3 = 2 (two elements failed ) and x 4 =3 (three elements failed). Failures of elements are independent of each other, the probabilities of failure of each element are equal, therefore it is applicable Bernoulli's formula
. Considering that, according to the condition, n=3, p=0.1, q=1-p=0.9, we determine the probabilities of the values:
P 3 (0) = C 3 0 p 0 q 3-0 = q 3 = 0.9 3 = 0.729;
P 3 (1) = C 3 1 p 1 q 3-1 = 3*0.1*0.9 2 = 0.243;
P 3 (2) = C 3 2 p 2 q 3-2 = 3*0.1 2 *0.9 = 0.027;
P 3 (3) = C 3 3 p 3 q 3-3 = p 3 =0.1 3 = 0.001;

Check: ∑p i = 0.729+0.243+0.027+0.001=1.

Thus, the desired binomial distribution law of X has the form:

3. We plot the possible values ​​of x i along the abscissa axis, and the corresponding probabilities p i along the ordinate axis. Let's construct points M 1 (0; 0.729), M 2 (1; 0.243), M 3 (2; 0.027), M 4 (3; 0.001). By connecting these points with straight line segments, we obtain the desired distribution polygon.

Let's find the distribution function F(x) = Р(Х<0) = 0;
For x ≤ 0 we have F(x) = Р(Х< x ≤1 имеем F(x) = Р(Х<1) = Р(Х = 0) = 0,729;
for 0< x ≤ 2 F(x) = Р(Х<2) = Р(Х=0) + Р(Х=1) =0,729+ 0,243 = 0,972;
for 1< x ≤ 3 F(x) = Р(Х<3) = Р(Х = 0) + Р(Х = 1) + Р(Х = 2) = 0,972+0,027 = 0,999;
for 2

for x > 3 there will be F(x) = 1, because the event is reliable.

4. Graph of function F(x)
For binomial distribution X:
- mathematical expectation M(X) = np = 3*0.1 = 0.3;
- variance D(X) = npq = 3*0.1*0.9 = 0.27;

- standard deviation σ(X) = √D(X) = √0.27 ≈ 0.52.

Section 6. Typical distribution laws and numerical characteristics of random variables
Secondly, very often random variables have similar distribution laws, i.e., for example, p(x) for them is expressed by formulas of the same form, differing only in one or more constants. These constants are called distribution parameters.

Although in principle a variety of distribution laws are possible, a few of the most typical laws will be considered here. It is important to pay attention to the conditions under which they arise, the parameters and properties of these distributions.

1 . Uniform distribution
This is the name given to the distribution of a random variable that can take any values ​​in the interval (a,b), and the probability of it falling into any segment inside (a,b) is proportional to the length of the segment and does not depend on its position, and the probability of values ​​outside (a,b ) is equal to 0.

Fig 6.1 Uniform distribution function and density

Distribution parameters: a, b

2. Normal distribution
Distribution with density described by the formula

(6.1)

called normal.
Distribution parameters: a, σ

Figure 6.2 Typical density and normal distribution function

3. Bernoulli distribution
If a series of independent trials is carried out, in each of which the event A can appear with the same probability p, then the number of occurrences of the event is a random variable distributed according to Bernoulli's law, or according to the binomial law (another name for distribution).

Here n is the number of trials in the series, m is a random variable (the number of occurrences of event A), P n (m) is the probability that A will occur exactly m times, q = 1 - p (the probability that A will not appear in the trial ).

Example 1: A die is rolled 5 times, what is the probability that a 6 will be rolled twice?
n = 5, m = 2, p = 1/6, q = 5/6

Distribution parameters: n, p

4 . Poisson distribution
The Poisson distribution is obtained as a limiting case of the Bernoulli distribution, if p tends to zero and n to infinity, but so that their product remains constant: nр = а. Formally, such a passage to the limit leads to the formula

Distribution parameter: a

Many random variables found in science and practical life are subject to the Poisson distribution.

Example 2: number of calls received at an ambulance station within an hour.
Let us divide the time interval T (1 hour) into small intervals dt, such that the probability of receiving two or more calls during dt is negligible, and the probability of one call p is proportional to dt: p = μdt;
we will consider observation during moments dt as independent trials, the number of such trials during time T: n = T / dt;
if we assume that the probabilities of call arrivals do not change during the hour, then the total number of calls obeys Bernoulli’s law with the parameters: n = T / dt, p = μdt. Having directed dt to zero, we find that n tends to infinity, and the product n×р remains constant: a = n×р = μT.

Example 3: the number of molecules of an ideal gas in some fixed volume V.
Let us divide the volume V into small volumes dV such that the probability of finding two or more molecules in dV is negligible, and the probability of finding one molecule is proportional to dV: p = μdV; we will consider the observation of each volume dV as an independent test, the number of such tests n=V/dV; if we assume that the probabilities of finding a molecule anywhere inside V are the same, the total number of molecules in volume V obeys Bernoulli's law with the parameters: n = V / dV, p = μdV. Having directed dV to zero, we find that n tends to infinity, and the product n×р remains constant: a = n×р =μV.

Numerical characteristics of random variables

1 . Mathematical expectation (average value)

Definition:
The mathematical expectation is called
  (6.4)

The sum is taken over all the values ​​that the random variable takes. The series must be absolutely convergent (otherwise the random variable is said to have no mathematical expectation)

;   (6.5)

The integral must be absolutely convergent (otherwise the random variable is said to have no mathematical expectation)

Properties of mathematical expectation:

a. If C is a constant value, then MC = C
b. MCx = CMx
c. The mathematical expectation of the sum of random variables is always equal to the sum of their mathematical expectations: M(x+y) = Mx + My d. The concept of conditional mathematical expectation is introduced. If a random variable takes its values ​​x i with different probabilities p(x i /H j) under different conditions H j, then the conditional expectation is determined

How or ;   (6.6)

If the probabilities of events H j are known, the complete

expected value: ;   (6.7)

Example 4: On average, how many times must a coin be tossed before the first symbol appears? This problem can be solved head-on

x i	1 2 3 ... k..
p(x i) :		,

but this amount still needs to be calculated. You can do it more simply by using the concepts of conditional and complete mathematical expectation. Let's consider hypotheses H 1 - the coat of arms fell out the first time, H 2 - the coat of arms did not fall out the first time. Obviously, p(H 1) = p(H 2) = ½; Mx / N 1 = 1;
Mx / N 2 is 1 more than the desired full expectation, because after the first toss of the coin the situation has not changed, but it has already been tossed once. Using the formula for the total mathematical expectation, we have Мх = Мx / Н 1 ×р(Н 1) + Мx / Н 2 ×р(Н 2) = 1 × 0.5 + (Мх + 1) × 0.5, solving the equation for Мх, we immediately obtain Mx = 2.

e. If f(x) is a function of a random variable x, then the concept of mathematical expectation of a function of a random variable is defined:

For a discrete random variable: ;   (6.8)

The sum is taken over all the values ​​that the random variable takes. The series must be absolutely convergent.

For a continuous random variable: ;   (6.9)

The integral must be absolutely convergent.

2. Variance of a random variable
Definition:
The variance of a random variable x is the mathematical expectation of the squared deviation of the value of the value from its mathematical expectation: Dx = M(x-Mx) 2

For a discrete random variable: ;   (6.10)

The sum is taken over all the values ​​that the random variable takes. The series must be convergent (otherwise the random variable is said to have no variance)

For a continuous random variable: ;   (6.11)

The integral must be convergent (otherwise the random variable is said to have no variance)

Dispersion properties:
a. If C is a constant value, then DC = 0
b. DСх = С 2 Dх
c. The variance of the sum of random variables is always equal to the sum of their variances only if these values ​​are independent (definition of independent variables)
d. To calculate the variance it is convenient to use the formula:

Dx = Mx 2 - (Mx) 2 (6.12)

Relationship between numerical characteristics
and parameters of typical distributions

distribution	options	formula	Mx	Dx
uniform	a, b		(b+a) / 2	(b-a) 2 / 12
normal	a, σ		a	σ 2
Bernoulli	n,p		n.p.	npq
Poisson	a		a	a